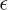| c | e | f | d
| 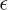
| Polynomial | G | I
| Galois
Slope
Content | GMS
| Deg 2
Subs
| Deg 4
Subs
|
|---|
| 0 | 1 | 8 | * | 1 | x8+x4+x3+x+ 1 | $C_{8}$
| <e>
|
| 0 | * | U4
|
|
|
| 8 | 2 | 4 | 1 | 1 | x8+ 28x4+ 144 | $C_4\times C_2$
| $C_2$ |
| 1 | *, -1, -* | U4
x4+ 8x2+ 4
x4-x2+ 5
|
| 8 | 2 | 4 | 1 | -1 | x8+ 2x7+ 8x2+ 48 | $(C_4\times C_2):C_2$
| $C_2^2$ |
| 3/2 | * | U4
x4+ 2x2+ 4x+ 4
x4- 5
|
| 8 | 2 | 4 | 1 | 1 | x8+ 2x7+ 2x6+ 16 | $((C_4\times C_2):C_2):C_2$
| $C_2^3$ |
| 7/4 | * | U4
|
| 8 | 2 | 4 | * | 1 | x8+ 2x7+ 2x6+ 8x3+ 48 | $C_{8}$
| $C_2$ |
| 1 | * | U4
|
| 8 | 2 | 4 | * | -1 | x8+ 2x7+ 8x2+ 16 | $C_8:C_2$
| $C_2^2$ |
| 3/2 | * | U4
|
| 8 | 2 | 4 | * | 1 | x8+ 2x7+ 2x6+ 16x2+ 16 | $(C_8:C_2):C_2$
| $C_2^3$ |
| 7/4 | * | U4
|
| 8 | 2 | 4 | -1 | i | x8+ 2x6+ 4x5+ 16 | $((C_8\times C_2):C_2):C_2$
| $C_2^4$ |
| 15/8 | * | U4
|
| 8 | 2 | 4 | -1 | -i | x8+ 4x5+ 8x2+ 48 | $((C_8\times C_2):C_2):C_2$
| $C_2^4$ |
| 15/8 | * | U4
|
| 8 | 2 | 4 | -* | i | x8+ 6x6+ 4x5+ 16 | $((C_8\times C_2):C_2):C_2$
| $C_2^4$ |
| 15/8 | * | U4
|
| 8 | 2 | 4 | -* | -i | x8+ 2x6+ 8x3+ 16 | $((C_8\times C_2):C_2):C_2$
| $C_2^4$ |
| 15/8 | * | U4
|
| 8 | 4 | 2 | 1 | 1 | x8+ 20x2+ 4 | $S_4$
| $A_4$ |
| 7/6 | * | x4+ 2x+ 2
|
| 8 | 4 | 2 | 1 | 1 | x8+ 2x5+ 2x4+ 4 | $A_4^2:C_2$
| $C_2^4:C_3$ |
| 31/24 | * |
|
| 8 | 8 | 1 | 1 | 1 | x8+ 2x+ 2 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 31/28 | |
|
|
|
| 10 | 8 | 1 | 1 | 1 | x8+ 2x3+ 2 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 19/14 | |
|
| 10 | 8 | 1 | * | 1 | x8+ 20x2+ 20 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 4/3 | | x4+ 2x+ 2
|
| 10 | 8 | 1 | * | 1 | x8+ 4x2+ 20 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 4/3 | | x4+ 2x+ 2
|
|
|
| 12 | 2 | 4 | 1 | -1 | x8+ 6x6+ 8x5+ 16 | $C_4\times C_2$
| $C_2$ |
| 3/2 | *, 2, 2* | U4
x4- 6x2+ 4
x4+ 2x2+ 20
|
| 12 | 2 | 4 | 1 | -1 | x8+ 2x6+ 8x4+ 16 | $C_4\times C_2$
| $C_2$ |
| 3/2 | *, -2, -2* | U4
x4- 2x2+ 4
x4- 2x2+ 20
|
| 12 | 2 | 4 | 1 | 1 | x8+ 2x6+ 16x2+ 16 | $(C_4\times C_2):C_2$
| $C_2^2$ |
| 2 | * | U4
x4+ 2x2- 4
x4- 20
|
| 12 | 2 | 4 | 1 | -1 | x8+ 2x6+ 16 | $((C_4\times C_2):C_2):C_2$
| $C_2^3$ |
| 9/4 | * | U4
|
| 12 | 2 | 4 | * | 1 | x8+ 6x6+ 8x5+ 80 | $C_{8}$
| $C_2$ |
| 3/2 | * | U4
|
| 12 | 2 | 4 | * | 1 | x8+ 2x6+ 8x4+ 80 | $C_{8}$
| $C_2$ |
| 3/2 | * | U4
|
| 12 | 2 | 4 | * | -1 | x8+ 4x6+ 8x2+ 80 | $C_8:C_2$
| $C_2^2$ |
| 2 | * | U4
|
| 12 | 2 | 4 | * | 1 | x8+ 2x6+ 80 | $(C_8:C_2):C_2$
| $C_2^3$ |
| 9/4 | * | U4
|
| 12 | 2 | 4 | -1 | i | x8+ 6x6+ 112 | $((C_8\times C_2):C_2):C_2$
| $C_2^4$ |
| 19/8 | * | U4
|
| 12 | 2 | 4 | -1 | -i | x8+ 2x6+ 112 | $((C_8\times C_2):C_2):C_2$
| $C_2^4$ |
| 19/8 | * | U4
|
| 12 | 2 | 4 | -* | -i | x8+ 6x6+ 48 | $((C_8\times C_2):C_2):C_2$
| $C_2^4$ |
| 19/8 | * | U4
|
| 12 | 2 | 4 | -* | i | x8+ 2x6+ 48 | $((C_8\times C_2):C_2):C_2$
| $C_2^4$ |
| 19/8 | * | U4
|
| 12 | 4 | 2 | 1 | 1 | x8+ 12x4+ 16 | $D_4$
| $C_2^2$ |
| 3/2 | *, -1, -* | x4+ 8x2+ 4
x4+ 2x2+ 4x+ 4
x4+ 2x3+ 2
|
| 12 | 4 | 2 | 1 | 1 | x8+ 12x4+ 144 | $D_4$
| $C_2^2$ |
| 3/2 | *, -1, -* | x4+ 8x2+ 4
x4- 5
x4+ 2x3+ 6
|
| 12 | 4 | 2 | 1 | 1 | x8+ 2x7+ 2x4+ 12 | $(C_4\times C_2):C_2$
| $C_2^2$ |
| 3/2 | * | x4-x2+ 5
x4+ 2x2+ 4x+ 4
x4- 5
|
| 12 | 4 | 2 | 1 | 1 | x8+ 24x2+ 4 | $A_4\times C_2$
| $C_2^2$ |
| 3/2 | * | x4+ 2x3+ 2x2+ 2
|
| 12 | 4 | 2 | 1 | -1 | x8+ 2x7+ 2x6+ 2x4+ 4 | $(C_2^4:C_3):C_2$
| $C_2^4$ |
| 15/8 | * |
|
| 12 | 4 | 2 | 1 | 1 | x8+ 8x7+ 48 | $(C_2^4:C_3):C_2$
| $C_2^4$ |
| 15/8 | * |
|
| 12 | 4 | 2 | * | -1 | x8+ 12x4+ 80 | $(C_8:C_2):C_2$
| $C_2^3$ |
| 7/4 | * | x4-x2+ 5
|
| 12 | 4 | 2 | * | -1 | x8+ 8x6+ 12x4+ 80 | $((C_4\times C_2):C_2):C_2$
| $C_2^3$ |
| 7/4 | *, -1, -* | x4+ 8x2+ 4
|
| 12 | 4 | 2 | * | 1 | x8+ 12x6+ 12x4+ 80 | T28
| $C_2^4$ |
| 15/8 | * | x4+ 2x2+ 4x+ 4
|
| 12 | 4 | 2 | * | -1 | x8+ 4x7+ 16x3+ 48 | T28
| $C_2^4$ |
| 15/8 | * | x4- 5
|
| 12 | 4 | 2 | * | -1 | x8+ 8x5+ 4x4+ 48 | T28
| $C_2^4$ |
| 15/8 | * | x4+ 2x2+ 4x+ 4
|
| 12 | 4 | 2 | * | 1 | x8+ 4x6+ 28x4+ 80 | T28
| $C_2^4$ |
| 15/8 | * | x4- 5
|
| 12 | 8 | 1 | 1 | 1 | x8+ 28x2+ 4 | $S_4\times C_2$
| $A_4\times C_2$
|
| 19/12 | -1 | x4+ 2x+ 2
|
| 12 | 8 | 1 | 1 | 1 | x8+ 12x2+ 4 | $S_4\times C_2$
| $A_4\times C_2$
|
| 19/12 | -* | x4+ 2x+ 2
|
| 12 | 8 | 1 | 1 | 1 | x8+ 4x5+ 4 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 45/28 | |
|
| 12 | 8 | 1 | 1 | 1 | x8+ 2x5+ 2 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 45/28 | |
|
| 12 | 8 | 1 | * | 1 | x8+ 28x2+ 20 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 19/12 | | x4+ 2x+ 2
|
| 12 | 8 | 1 | * | 1 | x8+ 12x2+ 20 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 19/12 | | x4+ 2x+ 2
|
|
|
| 14 | 8 | 1 | 1 | 1 | x8+ 2x7+ 6 | $A_4\times C_2$
| $C_2^3$
|
| 7/4 | -* | x4+ 2x3+ 2x2+ 2
|
| 14 | 8 | 1 | 1 | 1 | x8+ 2x7+ 2 | $A_4\times C_2$
| $C_2^3$
|
| 7/4 | -1 | x4+ 2x3+ 2x2+ 2
|
| 14 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x3+ 4 | $((C_4\times C_2):C_2):C_2$
| $C_2^3$
|
| 7/4 | -1 | x4+ 2x3+ 2
|
| 14 | 8 | 1 | 1 | 1 | x8+ 4x7+ 8x2+ 4 | $((C_4\times C_2):C_2):C_2$
| $C_2^3$
|
| 7/4 | -* | x4+ 2x3+ 6
|
| 14 | 8 | 1 | 1 | 1 | x8+ 2x7+ 2x6+ 2 | $C_2^3:C_7$
| $C_2^3$
|
| 7/4 | |
|
| 14 | 8 | 1 | 1 | 1 | x8+ 4x7+ 4 | $C_2^3:C_7$
| $C_2^3$
|
| 7/4 | |
|
| 14 | 8 | 1 | -1 | i | x8+ 28x2+ 28 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 5/2] | 2 | | 3 |
| 223/96 | | x4+ 2x+ 2
|
| 14 | 8 | 1 | -1 | -i | x8+ 20x2+ 28 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 5/2] | 2 | | 3 |
| 223/96 | | x4+ 2x+ 2
|
| 14 | 8 | 1 | -1 | i | x8+ 12x2+ 28 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 5/2] | 2 | | 3 |
| 223/96 | | x4+ 2x+ 2
|
| 14 | 8 | 1 | -1 | -i | x8+ 4x2+ 28 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 5/2] | 2 | | 3 |
| 223/96 | | x4+ 2x+ 2
|
| 14 | 8 | 1 | -* | -i | x8+ 20x2+ 12 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 5/2] | 2 | | 3 |
| 223/96 | | x4+ 2x+ 2
|
| 14 | 8 | 1 | -* | i | x8+ 12x2+ 12 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 5/2] | 2 | | 3 |
| 223/96 | | x4+ 2x+ 2
|
| 14 | 8 | 1 | -* | i | x8+ 28x2+ 12 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 5/2] | 2 | | 3 |
| 223/96 | | x4+ 2x+ 2
|
| 14 | 8 | 1 | -* | -i | x8+ 4x2+ 12 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 5/2] | 2 | | 3 |
| 223/96 | | x4+ 2x+ 2
|
|
|
| 16 | 4 | 2 | 1 | -1 | x8+ 6x6+ 2x4+ 4x2+ 8x+ 12 | $C_4\times C_2$
| $C_2^2$ |
| 2 | *, -2, -2* | x4-x2+ 5
x4- 2x2+ 4
x4+ 2x2+ 20
|
| 16 | 4 | 2 | 1 | 1 | x8+ 2x6+ 6x4+ 4x2+ 8x+ 20 | $C_4\times C_2$
| $C_2^2$ |
| 2 | *, -1, -* | x4+ 8x2+ 4
x4+ 2x2+ 20
x4- 2x2+ 20
|
| 16 | 4 | 2 | 1 | -1 | x8+ 2x6+ 6x4+ 4x2+ 8x+ 28 | $C_4\times C_2$
| $C_2^2$ |
| 2 | *, 2, 2* | x4-x2+ 5
x4- 6x2+ 4
x4- 2x2+ 20
|
| 16 | 4 | 2 | 1 | 1 | x8+ 6x6+ 6x4+ 8x3+ 4x2+ 8x+ 20 | $D_4$
| $C_2^2$ |
| 2 | *, -1, -* | x4+ 8x2+ 4
x4+ 2x2- 4
x4+ 6x2+ 4x+ 2
|
| 16 | 4 | 2 | 1 | 1 | x8+ 4x6+ 40x2+ 4 | $D_4$
| $C_2^2$ |
| 2 | *, -1, -* | x4+ 8x2+ 4
x4- 20
x4+ 2x2+ 4x+ 6
|
| 16 | 4 | 2 | 1 | 1 | x8+ 4x6+ 8x2+ 4 | $C_2^3$
| $C_2^2$ |
| 2 | *, -1, -*, -2, -2*, 2, 2* | x4+ 8x2+ 4
x4- 6x2+ 4
x4- 2x2+ 4
x4+ 6x2+ 4x+ 6
x4+ 6x2+ 4x+ 14
x4+ 6x2+ 1
x4+ 2x2+ 4x+ 10
|
| 16 | 4 | 2 | 1 | -1 | x8+ 6x6+ 6x4+ 12x2+ 8x+ 12 | $(C_4\times C_2):C_2$
| $C_2^2$ |
| 2 | * | x4-x2+ 5
x4+ 2x2- 4
x4- 20
|
| 16 | 4 | 2 | 1 | 1 | x8+ 8x5+ 12 | $S_4$
| $A_4$ |
| 13/6 | * | x4+ 4x+ 2
|
| 16 | 4 | 2 | 1 | 1 | x8+ 2x4+ 8x+ 12 | $S_4$
| $A_4$ |
| 13/6 | * | x4+ 4x2+ 4x+ 2
|
| 16 | 4 | 2 | 1 | -1 | x8+ 2x6+ 4x5+ 6x4+ 4 | $D_4\times C_2$
| $C_2^3$ |
| 9/4 | *, -2, -2* | x4- 5
x4- 2x2+ 4
x4- 20
|
| 16 | 4 | 2 | 1 | 1 | x8+ 4x7+ 2x6+ 4x5+ 2x4+ 4 | $D_4\times C_2$
| $C_2^3$ |
| 9/4 | *, -2, -2* | x4+ 2x2+ 4x+ 4
x4- 2x2+ 4
x4+ 2x2- 4
|
| 16 | 4 | 2 | 1 | 1 | x8+ 6x6+ 4x5+ 2x4+ 12 | $(C_4\times C_2):C_2$
| $C_2^3$ |
| 9/4 | * | x4- 5
x4+ 2x2+ 20
x4+ 2x2- 4
|
| 16 | 4 | 2 | 1 | -1 | x8+ 6x6+ 4x5+ 2x4+ 4 | $D_4\times C_2$
| $C_2^3$ |
| 9/4 | *, 2, 2* | x4+ 2x2+ 4x+ 4
x4- 6x2+ 4
x4+ 2x2- 4
|
| 16 | 4 | 2 | 1 | -1 | x8+ 2x6+ 4x5+ 6x4+ 8x2+ 12 | $(C_4\times C_2):C_2$
| $C_2^3$ |
| 9/4 | * | x4+ 2x2+ 4x+ 4
x4+ 2x2+ 20
x4- 20
|
| 16 | 4 | 2 | 1 | 1 | x8+ 4x6+ 4x5+ 2x4+ 12x2+ 8x+ 28 | $(C_4\times C_2):C_2$
| $C_2^3$ |
| 9/4 | * | x4+ 2x2+ 4x+ 4
x4- 2x2+ 20
x4- 20
|
| 16 | 4 | 2 | 1 | 1 | x8+ 2x6+ 4x5+ 6x4+ 8x3+ 4 | $D_4\times C_2$
| $C_2^3$ |
| 9/4 | *, 2, 2* | x4- 5
x4- 6x2+ 4
x4- 20
|
| 16 | 4 | 2 | 1 | -1 | x8+ 2x6+ 4x5+ 6x4+ 20 | $(C_4\times C_2):C_2$
| $C_2^3$ |
| 9/4 | * | x4- 5
x4- 2x2+ 20
x4+ 2x2- 4
|
| 16 | 4 | 2 | 1 | -1 | x8+ 2x4+ 8x2+ 8x+ 4 | $(C_2^4:C_3):C_2$
| $C_2^4:C_3$ |
| 55/24 | * |
|
| 16 | 4 | 2 | 1 | -1 | x8+ 12x7+ 20x5+ 16x4+ 40x+ 20 | $(C_4\times C_2):C_2$
| $C_4\times C_2$ |
| 5/2 | *, -1, -* | x4+ 8x2+ 4
|
| 16 | 4 | 2 | 1 | 1 | x8+ 4x6+ 4x4+ 16 | $(C_4\times C_2):C_2$
| $C_4\times C_2$ |
| 5/2 | *, -1, -* | x4+ 8x2+ 4
|
| 16 | 4 | 2 | 1 | 1 | x8+ 12x6+ 4x4+ 16 | $(C_4\times C_2):C_2$
| $C_4\times C_2$ |
| 5/2 | *, -1, -* | x4+ 8x2+ 4
|
| 16 | 4 | 2 | 1 | -1 | x8+ 2x6+ 4x5+ 10x4+ 8x3+ 12x2+ 4 | $(C_4\times C_2):C_2$
| $C_4\times C_2$ |
| 5/2 | *, -1, -* | x4+ 8x2+ 4
|
| 16 | 4 | 2 | 1 | -1 | x8+ 4x6+ 20x4+ 16 | $((C_4\times C_2):C_2):C_2$
| $C_4\times C_2$ |
| 5/2 | * | x4-x2+ 5
|
| 16 | 4 | 2 | 1 | 1 | x8+ 2x6+ 4x5+ 2x4+ 12x2+ 12 | $((C_4\times C_2):C_2):C_2$
| $C_4\times C_2$ |
| 5/2 | * | x4-x2+ 5
|
| 16 | 4 | 2 | 1 | 1 | x8+ 4x5+ 6x4+ 12 | $A_4^2:C_2$
| $C_2^4:C_3$ |
| 61/24 | * |
|
| 16 | 4 | 2 | 1 | -1 | x8+ 4x5+ 24x+ 12 | $A_4^2:C_2$
| $C_2^4:C_3$ |
| 61/24 | * |
|
| 16 | 4 | 2 | 1 | -1 | x8+ 4x5+ 8x+ 12 | $A_4^2:C_2$
| $C_2^4:C_3$ |
| 61/24 | * |
|
| 16 | 4 | 2 | 1 | 1 | x8+ 4x5+ 6x4+ 4 | $A_4^2:C_2$
| $C_2^4:C_3$ |
| 61/24 | * |
|
| 16 | 4 | 2 | * | -1 | x8+ 2x6+ 2x4+ 4x2+ 8x+ 12 | $(C_8:C_2):C_2$
| $C_2^3$ |
| 9/4 | * | x4-x2+ 5
|
| 16 | 4 | 2 | * | 1 | x8+ 8x7+ 20 | $((C_4\times C_2):C_2):C_2$
| $C_2^3$ |
| 9/4 | *, -1, -* | x4+ 8x2+ 4
|
| 16 | 4 | 2 | * | -1 | x8+ 2x6+ 4x5+ 2x4+ 8x3+ 4 | T28
| $C_2^4$ |
| 19/8 | * | x4+ 2x2+ 4x+ 4
|
| 16 | 4 | 2 | * | -1 | x8+ 6x6+ 4x5+ 6x4+ 8x3+ 4 | T28
| $C_2^4$ |
| 19/8 | * | x4- 5
|
| 16 | 4 | 2 | * | 1 | x8+ 6x6+ 4x5+ 6x4+ 4 | T28
| $C_2^4$ |
| 19/8 | * | x4- 5
|
| 16 | 4 | 2 | * | 1 | x8+ 2x6+ 4x5+ 2x4+ 4 | T28
| $C_2^4$ |
| 19/8 | * | x4+ 2x2+ 4x+ 4
|
| 16 | 4 | 2 | * | 1 | x8+ 6x6+ 4x5+ 10x4+ 4x2+ 12 | $C_8:C_2$
| $C_4\times C_2$ |
| 5/2 | * | x4-x2+ 5
|
| 16 | 4 | 2 | * | -1 | x8+ 4x6+ 20x4+ 208 | $C_8:C_2$
| $C_4\times C_2$ |
| 5/2 | * | x4-x2+ 5
|
| 16 | 4 | 2 | * | 1 | x8+ 6x6+ 4x5+ 2x4+ 4x2+ 12 | $C_8:C_2$
| $C_4\times C_2$ |
| 5/2 | * | x4-x2+ 5
|
| 16 | 4 | 2 | * | -1 | x8+ 2x6+ 4x5+ 2x4+ 4x2+ 12 | $C_8:C_2$
| $C_4\times C_2$ |
| 5/2 | * | x4-x2+ 5
|
| 16 | 4 | 2 | * | -1 | x8+ 2x6+ 4x5+ 2x4+ 4x2+ 4 | $((C_4\times C_2):C_2):C_2$
| $C_4\times C_2$ |
| 5/2 | *, -1, -* | x4+ 8x2+ 4
|
| 16 | 4 | 2 | * | 1 | x8+ 4x6+ 4x4+ 80 | $((C_4\times C_2):C_2):C_2$
| $C_4\times C_2$ |
| 5/2 | *, -1, -* | x4+ 8x2+ 4
|
| 16 | 4 | 2 | -1 | i | x8+ 4x7+ 2x6+ 8x4+ 4x2+ 4 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 21/8 | * | x4+ 2x2+ 4x+ 4
|
| 16 | 4 | 2 | -1 | i | x8+ 4x4+ 112 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 21/8 | * | x4+ 2x2+ 4x+ 4
|
| 16 | 4 | 2 | -1 | i | x8+ 4x4+ 240 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 21/8 | * | x4+ 2x2+ 4x+ 4
|
| 16 | 4 | 2 | -1 | i | x8+ 4x4+ 16x2+ 112 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 21/8 | * | x4+ 2x2+ 4x+ 4
|
| 16 | 4 | 2 | -1 | i | x8+ 8x6+ 4x4+ 240 | T30
| $D_4\times C_2$ |
| 21/8 | * | x4- 5
|
| 16 | 4 | 2 | -1 | i | x8+ 24x6+ 4x4+ 240 | T30
| $D_4\times C_2$ |
| 21/8 | * | x4- 5
|
| 16 | 4 | 2 | -1 | -i | x8+ 20x4+ 16x2+ 112 | T30
| $D_4\times C_2$ |
| 21/8 | * | x4- 5
|
| 16 | 4 | 2 | -1 | -i | x8+ 4x6+ 12x4+ 112 | T30
| $D_4\times C_2$ |
| 21/8 | * | x4- 5
|
| 16 | 4 | 2 | -* | -i | x8+ 14x4+ 12x2+ 8x+ 4 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 21/8 | * | x4- 5
|
| 16 | 4 | 2 | -* | -i | x8+ 48 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 21/8 | * | x4- 5
|
| 16 | 4 | 2 | -* | -i | x8+ 3 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 21/8 | * | x4- 5
|
| 16 | 4 | 2 | -* | -i | x8+ 4x4+ 48 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 21/8 | * | x4- 5
|
| 16 | 4 | 2 | -* | i | x8+ 4x6+ 28x4+ 48 | T30
| $D_4\times C_2$ |
| 21/8 | * | x4+ 2x2+ 4x+ 4
|
| 16 | 4 | 2 | -* | -i | x8+ 16x5+ 20x4+ 112 | T30
| $D_4\times C_2$ |
| 21/8 | * | x4+ 2x2+ 4x+ 4
|
| 16 | 4 | 2 | -* | i | x8+ 4x7+ 10x6+ 20x2+ 4 | T30
| $D_4\times C_2$ |
| 21/8 | * | x4+ 2x2+ 4x+ 4
|
| 16 | 4 | 2 | -* | -i | x8+ 24x6+ 4x4+ 48 | T30
| $D_4\times C_2$ |
| 21/8 | * | x4+ 2x2+ 4x+ 4
|
| 16 | 8 | 1 | 1 | -1 | x8+ 14x6+ 4 | $S_4\times C_2$
| $A_4\times C_2$
|
| 25/12 | -2 | x4+ 2x+ 2
|
| 16 | 8 | 1 | 1 | -1 | x8+ 2x6+ 4 | $S_4\times C_2$
| $A_4\times C_2$
|
| 25/12 | 2 | x4+ 2x+ 2
|
| 16 | 8 | 1 | 1 | -1 | x8+ 6x6+ 4 | $S_4\times C_2$
| $A_4\times C_2$
|
| 25/12 | -2* | x4+ 2x+ 2
|
| 16 | 8 | 1 | 1 | -1 | x8+ 10x6+ 4 | $S_4\times C_2$
| $A_4\times C_2$
|
| 25/12 | 2* | x4+ 2x+ 2
|
| 16 | 8 | 1 | 1 | 1 | x8+ 4x+ 2 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 59/28 | |
|
| 16 | 8 | 1 | 1 | 1 | x8+ 4x+ 6 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 59/28 | |
|
| 16 | 8 | 1 | 1 | 1 | x8+ 8x5+ 20 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 2, 7/3, 7/3] | 2 | | 3 |
| 103/48 | -* |
|
| 16 | 8 | 1 | 1 | 1 | x8+ 8x5+ 4 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 2, 7/3, 7/3] | 2 | | 3 |
| 103/48 | -1 |
|
| 16 | 8 | 1 | * | 1 | x8+ 4x6+ 28x4+ 20 | $QD_{16}$
| $Q_8$
|
| 2 | -1 | x4+ 2x3+ 2
|
| 16 | 8 | 1 | * | 1 | x8+ 8x4+ 336 | $QD_{16}$
| $Q_8$
|
| 2 | -* | x4+ 2x3+ 6
|
| 16 | 8 | 1 | * | 1 | x8+ 8x4+ 80 | $C_4^2:C_2$
| $Q_8$
|
| 2 | -1 | x4+ 2x3+ 2
|
| 16 | 8 | 1 | * | 1 | x8+ 2x6+ 4x+ 6 | $C_4^2:C_2$
| $Q_8$
|
| 2 | -* | x4+ 2x3+ 6
|
| 16 | 8 | 1 | * | 1 | x8+ 12x6+ 28x4+ 52 | $C_4^2:C_2$
| $Q_8$
|
| 2 | -1 | x4+ 2x3+ 2
|
| 16 | 8 | 1 | * | 1 | x8+ 8x3+ 8x2+ 24 | $C_4^2:C_2$
| $Q_8$
|
| 2 | -* | x4+ 2x3+ 6
|
| 16 | 8 | 1 | * | 1 | x8+ 6x6+ 20 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 25/12 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | * | 1 | x8+ 10x6+ 20 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 25/12 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | * | 1 | x8+ 2x6+ 20 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 25/12 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | * | 1 | x8+ 14x6+ 20 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 25/12 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | * | -1 | x8+ 8x2+ 52 | T38
| T22
|
| 35/16 | | x4+ 2x3+ 2x2+ 2
|
| 16 | 8 | 1 | * | -1 | x8+ 8x2+ 20 | T38
| T22
|
| 35/16 | | x4+ 2x3+ 2x2+ 2
|
| 16 | 8 | 1 | * | -1 | x8+ 8x6+ 8x2+ 20 | T38
| T22
|
| 35/16 | | x4+ 2x3+ 2x2+ 2
|
| 16 | 8 | 1 | * | -1 | x8+ 56x2+ 52 | T38
| T22
|
| 35/16 | | x4+ 2x3+ 2x2+ 2
|
| 16 | 8 | 1 | -1 | i | x8+ 14x6+ 28 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 3] | 2 | | 3 |
| 247/96 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | -1 | -i | x8+ 10x6+ 28 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 3] | 2 | | 3 |
| 247/96 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | -1 | -i | x8+ 2x6+ 28 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 3] | 2 | | 3 |
| 247/96 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | -1 | i | x8+ 6x6+ 28 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 3] | 2 | | 3 |
| 247/96 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | -* | i | x8+ 10x6+ 12 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 3] | 2 | | 3 |
| 247/96 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | -* | -i | x8+ 14x6+ 12 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 3] | 2 | | 3 |
| 247/96 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | -* | i | x8+ 2x6+ 12 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 3] | 2 | | 3 |
| 247/96 | | x4+ 2x+ 2
|
| 16 | 8 | 1 | -* | -i | x8+ 6x6+ 12 | T44
| T38
|
| [4/3, 4/3, 2, 7/3, 7/3, 3] | 2 | | 3 |
| 247/96 | | x4+ 2x+ 2
|
|
|
| 17 | 8 | 1 | 2 | 1 | x8+ 14x6+ 8 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2 | 1 | x8+ 10x2+ 2 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2 | -1 | x8+ 6x6+ 8 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2 | -1 | x8+ 14x2+ 2 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2 | 1 | x8+ 2x6+ 8 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2 | -1 | x8+ 2x2+ 2 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2 | 1 | x8+ 6x2+ 2 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2 | -1 | x8+ 10x6+ 8 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2* | 1 | x8+ 6x2+ 10 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2* | -1 | x8+ 2x2+ 10 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2* | -1 | x8+ 14x2+ 10 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2* | 1 | x8+ 2x6+ 40 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2* | 1 | x8+ 10x2+ 10 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2* | 1 | x8+ 14x6+ 40 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2* | -1 | x8+ 10x6+ 40 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | 2* | -1 | x8+ 6x6+ 40 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2 | -i | x8+ 14x6+ 56 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2 | -i | x8+ 10x2+ 14 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2 | i | x8+ 6x6+ 56 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2 | i | x8+ 2x2+ 14 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2 | -i | x8+ 10x6+ 56 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2 | i | x8+ 6x2+ 14 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2 | -i | x8+ 14x2+ 14 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2 | i | x8+ 2x6+ 56 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2* | -i | x8+ 14x2+ 6 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2* | i | x8+ 2x2+ 6 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2* | -i | x8+ 14x6+ 24 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2* | -i | x8+ 10x2+ 6 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2* | i | x8+ 6x2+ 6 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2* | i | x8+ 2x6+ 24 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2* | -i | x8+ 10x6+ 24 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
| 17 | 8 | 1 | -2* | i | x8+ 6x6+ 24 | T44
| T38
|
| [4/3, 4/3, 3, 19/6, 19/6, 13/4] | 2 | | 3 |
| 295/96 | | x4+ 2x+ 2
|
|
|
| 18 | 4 | 2 | 1 | -1 | x8+ 14x6+ 10x4+ 12x2+ 16x+ 4 | $D_4\times C_2$
| $D_4$ |
| 11/4 | *, -1, -* | x4+ 8x2+ 4
x4- 2x2+ 2
x4+ 6x2+ 2
|
| 18 | 4 | 2 | 1 | 1 | x8+ 24x4+ 36 | $D_4\times C_2$
| $D_4$ |
| 11/4 | *, -1, -* | x4+ 8x2+ 4
x4+ 2x2+ 6
x4- 2x2+ 6
|
| 18 | 4 | 2 | 1 | -1 | x8+ 14x6+ 10x4+ 8x3+ 12x2+ 20 | $(C_4\times C_2):C_2$
| $D_4$ |
| 11/4 | *, -1, -* | x4+ 8x2+ 4
|
| 18 | 4 | 2 | 1 | -1 | x8+ 10x6+ 10x4+ 4x2+ 4 | $D_4\times C_2$
| $D_4$ |
| 11/4 | *, -1, -* | x4+ 8x2+ 4
x4+ 6x2+ 10
x4+ 2x2+ 10
|
| 18 | 4 | 2 | 1 | -1 | x8+ 2x6+ 14x4+ 20x2+ 4 | $(C_4\times C_2):C_2$
| $D_4$ |
| 11/4 | *, -1, -* | x4+ 8x2+ 4
|
| 18 | 4 | 2 | 1 | 1 | x8+ 16x4+ 4 | $(C_4\times C_2):C_2$
| $D_4$ |
| 11/4 | *, -1, -* | x4+ 8x2+ 4
|
| 18 | 4 | 2 | 1 | 1 | x8+ 8x4+ 4 | $D_4\times C_2$
| $D_4$ |
| 11/4 | *, -1, -* | x4+ 8x2+ 4
x4+ 2x2- 2
x4- 2x2- 2
|
| 18 | 4 | 2 | 1 | 1 | x8+ 36 | $(C_4\times C_2):C_2$
| $D_4$ |
| 11/4 | *, -1, -* | x4+ 8x2+ 4
|
| 18 | 4 | 2 | 1 | -1 | x8+ 2x6+ 6x4+ 4 | T29
| $C_2^4:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | 1 | -1 | x8+ 2x6+ 20x2+ 4 | T29
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | 1 | 1 | x8+ 2x4+ 12x2+ 4 | T29
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | 1 | 1 | x8+ 6x6+ 10x4+ 4 | T29
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | 1 | -1 | x8+ 2x6+ 2x4+ 4 | T29
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | 1 | -1 | x8+ 2x6+ 14x4+ 4 | T29
| $C_2^4:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | 1 | 1 | x8+ 6x4+ 4x2+ 4 | T29
| $C_2^4:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | 1 | 1 | x8+ 6x6+ 4x2+ 4 | T29
| $C_2^4:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | * | 1 | x8+ 16x2+ 20 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$ |
| 23/8 | *, -1, -* | x4+ 8x2+ 4
|
| 18 | 4 | 2 | * | -1 | x8+ 8x6+ 52 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$ |
| 23/8 | *, -1, -* | x4+ 8x2+ 4
|
| 18 | 4 | 2 | * | 1 | x8+ 16x5+ 36 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$ |
| 23/8 | *, -1, -* | x4+ 8x2+ 4
|
| 18 | 4 | 2 | * | -1 | x8+ 4x7+ 2x6+ 10x4+ 20x2+ 4 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$ |
| 23/8 | *, -1, -* | x4+ 8x2+ 4
|
| 18 | 4 | 2 | * | -1 | x8+ 10x4+ 4x2+ 20 | T28
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | * | 1 | x8+ 2x6+ 2x4+ 20 | T28
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | * | 1 | x8+ 14x4+ 4x2+ 20 | T28
| $C_2^4:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | * | -1 | x8+ 6x6+ 6x4+ 20 | T28
| $C_2^4:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | * | -1 | x8+ 6x6+ 14x4+ 20 | T28
| $C_2^4:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | * | 1 | x8+ 10x6+ 12x2+ 20 | T28
| $C_2^4:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | * | -1 | x8+ 6x6+ 2x4+ 20 | T28
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | * | 1 | x8+ 10x4+ 12x2+ 20 | T28
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | -1 | i | x8+ 12x6+ 28x4+ 28 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 3 | * | x4-x2+ 5
|
| 18 | 4 | 2 | -1 | -i | x8+ 6x6+ 2x4+ 4x2+ 28 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 3 | * | x4-x2+ 5
|
| 18 | 4 | 2 | -1 | -i | x8+ 20x4+ 16x3+ 24x2+ 60 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 3 | * | x4-x2+ 5
|
| 18 | 4 | 2 | -1 | i | x8+ 12x6+ 12x4+ 28 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 3 | * | x4-x2+ 5
|
| 18 | 4 | 2 | -1 | i | x8+ 2x6+ 14x4+ 28 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | -1 | -i | x8+ 2x6+ 8x5+ 6x4+ 28 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | -1 | i | x8+ 2x6+ 6x4+ 28 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | -1 | -i | x8+ 2x6+ 8x5+ 14x4+ 28 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | -1 | -i | x8+ 6x4+ 4x2+ 28 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | -1 | i | x8+ 6x6+ 2x4+ 28 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | -1 | -i | x8+ 14x4+ 4x2+ 28 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | -1 | i | x8+ 2x6+ 2x4+ 28 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | -* | -i | x8+ 4x6+ 20x4+ 44 | $((C_8\times C_2):C_2):C_2$
| $(C_4\times C_2): C_2$ |
| 3 | * | x4-x2+ 5
|
| 18 | 4 | 2 | -* | -i | x8+ 4x6+ 4x4+ 44 | $((C_8\times C_2):C_2):C_2$
| $(C_4\times C_2): C_2$ |
| 3 | * | x4-x2+ 5
|
| 18 | 4 | 2 | -* | i | x8+ 12x4+ 8x2+ 44 | $((C_8\times C_2):C_2):C_2$
| $(C_4\times C_2): C_2$ |
| 3 | * | x4-x2+ 5
|
| 18 | 4 | 2 | -* | i | x8+ 12x6+ 4x4+ 12 | $((C_8\times C_2):C_2):C_2$
| $(C_4\times C_2): C_2$ |
| 3 | * | x4-x2+ 5
|
| 18 | 4 | 2 | -* | -i | x8+ 6x4+ 12x2+ 12 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | -* | i | x8+ 6x6+ 10x4+ 16x2+ 12 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | -* | i | x8+ 4x7+ 2x6+ 8x5+ 2x4+ 28 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | -* | -i | x8+ 6x6+ 2x4+ 12 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4- 5
|
| 18 | 4 | 2 | -* | i | x8+ 10x4+ 4x2+ 12 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | -* | i | x8+ 10x4+ 12x2+ 12 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | -* | -i | x8+ 2x6+ 14x4+ 12 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 4 | 2 | -* | -i | x8+ 2x6+ 6x4+ 12 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2+ 4x+ 4
|
| 18 | 8 | 1 | 1 | -1 | x8+ 2x6+ 4x3+ 2 | $D_4\times C_2$
| $C_2^3$
|
| 9/4 | -1, -2, 2 | x4+ 2x3+ 2
x4+ 6x2+ 1
x4+ 6x2+ 4x+ 2
|
| 18 | 8 | 1 | 1 | -1 | x8+ 6x6+ 4x3+ 6 | $D_4\times C_2$
| $C_2^3$
|
| 9/4 | -*, -2, 2* | x4+ 2x3+ 6
x4+ 6x2+ 4x+ 6
x4+ 2x2+ 4x+ 6
|
| 18 | 8 | 1 | 1 | -1 | x8+ 2x6+ 4x3+ 10 | $D_4\times C_2$
| $C_2^3$
|
| 9/4 | -1, -2*, 2* | x4+ 2x3+ 2
x4+ 2x2+ 4x+ 10
x4+ 6x2+ 4x+ 2
|
| 18 | 8 | 1 | 1 | -1 | x8+ 168x4+ 912 | $D_4\times C_2$
| $C_2^3$
|
| 9/4 | -*, -2*, 2 | x4+ 2x3+ 6
x4+ 6x2+ 4x+ 14
x4+ 2x2+ 4x+ 6
|
| 18 | 8 | 1 | 1 | 1 | x8+ 12x6+ 36 | $A_4\times C_2$
| $C_2^3$
|
| 9/4 | -2* | x4+ 2x3+ 2x2+ 2
|
| 18 | 8 | 1 | 1 | 1 | x8+ 12x6+ 4 | $A_4\times C_2$
| $C_2^3$
|
| 9/4 | 2* | x4+ 2x3+ 2x2+ 2
|
| 18 | 8 | 1 | 1 | 1 | x8+ 4x6+ 4 | $A_4\times C_2$
| $C_2^3$
|
| 9/4 | -2 | x4+ 2x3+ 2x2+ 2
|
| 18 | 8 | 1 | 1 | 1 | x8+ 4x6+ 36 | $A_4\times C_2$
| $C_2^3$
|
| 9/4 | 2 | x4+ 2x3+ 2x2+ 2
|
| 18 | 8 | 1 | 1 | -1 | x8+ 6x6+ 4x3+ 2 | $((C_4\times C_2):C_2):C_2$
| $C_2^3$
|
| 9/4 | -1 | x4+ 2x3+ 2
|
| 18 | 8 | 1 | 1 | -1 | x8+ 2x6+ 4x3+ 6 | $((C_4\times C_2):C_2):C_2$
| $C_2^3$
|
| 9/4 | -* | x4+ 2x3+ 6
|
| 18 | 8 | 1 | 1 | 1 | x8+ 2x4+ 4x3+ 6 | $S_4\times C_2$
| $A_4\times C_2$
|
| 7/3 | -* | x4+ 4x2+ 4x+ 2
|
| 18 | 8 | 1 | 1 | 1 | x8+ 2x4+ 4x3+ 2 | $S_4\times C_2$
| $A_4\times C_2$
|
| 7/3 | -1 | x4+ 4x+ 2
|
| 18 | 8 | 1 | 1 | 1 | x8+ 6x4+ 4x3+ 6 | $S_4\times C_2$
| $A_4\times C_2$
|
| 7/3 | -* | x4+ 4x+ 2
|
| 18 | 8 | 1 | 1 | 1 | x8+ 6x4+ 4x3+ 2 | $S_4\times C_2$
| $A_4\times C_2$
|
| 7/3 | -1 | x4+ 4x2+ 4x+ 2
|
| 18 | 8 | 1 | 1 | 1 | x8+ 4x3+ 2 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 33/14 | |
|
| 18 | 8 | 1 | 1 | 1 | x8+ 4x3+ 4x2+ 2 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 33/14 | |
|
| 18 | 8 | 1 | 1 | 1 | x8+ 4x4+ 4x3+ 2 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 33/14 | |
|
| 18 | 8 | 1 | 1 | 1 | x8+ 4x3+ 4x2+ 6 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 33/14 | |
|
| 18 | 8 | 1 | 1 | -1 | x8+ 2x4+ 4x3+ 4x2+ 2 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 2, 8/3, 8/3] | 2 | | 3 |
| 115/48 | -1 |
|
| 18 | 8 | 1 | 1 | -1 | x8+ 2x4+ 4x3+ 4x2+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 2, 8/3, 8/3] | 2 | | 3 |
| 115/48 | -* |
|
| 18 | 8 | 1 | * | 1 | x8+ 56x4+ 80 | $QD_{16}$
| $Q_8$
|
| 9/4 | -* | x4+ 2x3+ 6
|
| 18 | 8 | 1 | * | 1 | x8+ 8x7+ 4 | $QD_{16}$
| $Q_8$
|
| 9/4 | -1 | x4+ 2x3+ 2
|
| 18 | 8 | 1 | * | 1 | x8+ 24x4+ 208 | $C_4^2:C_2$
| $Q_8$
|
| 9/4 | -1 | x4+ 2x3+ 2
|
| 18 | 8 | 1 | * | 1 | x8+ 8x7+ 24x6+ 20 | $C_4^2:C_2$
| $Q_8$
|
| 9/4 | -* | x4+ 2x3+ 6
|
| 18 | 8 | 1 | * | 1 | x8+ 8x7+ 36 | $C_4^2:C_2$
| $Q_8$
|
| 9/4 | -1 | x4+ 2x3+ 2
|
| 18 | 8 | 1 | * | 1 | x8+ 2x6+ 4x5+ 4x3+ 14 | $C_4^2:C_2$
| $Q_8$
|
| 9/4 | -* | x4+ 2x3+ 6
|
| 18 | 8 | 1 | * | 1 | x8+ 28x6+ 52 | T38
| T22
|
| 39/16 | | x4+ 2x3+ 2x2+ 2
|
| 18 | 8 | 1 | * | 1 | x8+ 12x6+ 20 | T38
| T22
|
| 39/16 | | x4+ 2x3+ 2x2+ 2
|
| 18 | 8 | 1 | * | 1 | x8+ 28x6+ 20 | T38
| T22
|
| 39/16 | | x4+ 2x3+ 2x2+ 2
|
| 18 | 8 | 1 | * | 1 | x8+ 4x6+ 20 | T38
| T22
|
| 39/16 | | x4+ 2x3+ 2x2+ 2
|
|
|
| 20 | 4 | 2 | 1 | -1 | x8+ 4x7+ 14x4+ 4 | $D_4\times C_2$
| $D_4$ |
| 11/4 | *, 2, 2* | x4- 6x2+ 4
x4+ 6x2- 9
x4+ 2x2- 1
|
| 20 | 4 | 2 | 1 | 1 | x8+ 4x7+ 8x6+ 2x4+ 4 | $(C_4\times C_2):C_2$
| $D_4$ |
| 11/4 | *, -2, -2* | x4- 2x2+ 4
|
| 20 | 4 | 2 | 1 | -1 | x8+ 4x7+ 6x4+ 4 | $D_4\times C_2$
| $D_4$ |
| 11/4 | *, 2, 2* | x4- 6x2+ 4
x4+ 6x2- 1
x4+ 2x2- 9
|
| 20 | 4 | 2 | 1 | 1 | x8+ 72x4+ 656 | $(C_4\times C_2):C_2$
| $D_4$ |
| 11/4 | *, 2, 2* | x4- 6x2+ 4
|
| 20 | 4 | 2 | 1 | -1 | x8+ 40x4+ 528 | $D_4\times C_2$
| $D_4$ |
| 11/4 | *, -2, -2* | x4- 2x2+ 4
x4+ 6x2+ 3
x4- 6x2+ 3
|
| 20 | 4 | 2 | 1 | 1 | x8+ 4x7+ 8x6+ 10x4+ 4 | $(C_4\times C_2):C_2$
| $D_4$ |
| 11/4 | *, -2, -2* | x4- 2x2+ 4
|
| 20 | 4 | 2 | 1 | 1 | x8+ 72x4+ 144 | $(C_4\times C_2):C_2$
| $D_4$ |
| 11/4 | *, 2, 2* | x4- 6x2+ 4
|
| 20 | 4 | 2 | 1 | -1 | x8+ 4x7+ 10x4+ 4 | $D_4\times C_2$
| $D_4$ |
| 11/4 | *, -2, -2* | x4- 2x2+ 4
x4+ 2x2+ 3
x4- 2x2+ 3
|
| 20 | 4 | 2 | 1 | -1 | x8+ 4x7+ 6x4+ 20 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$ |
| 23/8 | * | x4+ 2x2+ 20
|
| 20 | 4 | 2 | 1 | -1 | x8+ 4x7+ 2x4+ 20 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$ |
| 23/8 | * | x4- 2x2+ 20
|
| 20 | 4 | 2 | 1 | 1 | x8+ 4x7+ 4x6+ 6x4+ 24x2+ 20 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$ |
| 23/8 | * | x4- 2x2+ 20
|
| 20 | 4 | 2 | 1 | 1 | x8+ 4x7+ 12x6+ 2x4+ 24x2+ 20 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$ |
| 23/8 | * | x4+ 2x2+ 20
|
| 20 | 4 | 2 | * | -1 | x8+ 4x7+ 10x4+ 8x2+ 4 | T28
| $(C_4\times C_2): C_2$ |
| 3 | * | x4- 20
|
| 20 | 4 | 2 | * | -1 | x8+ 4x7+ 8x6+ 10x4+ 12 | T28
| $(C_4\times C_2): C_2$ |
| 3 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | * | -1 | x8+ 4x7+ 12x6+ 8x5+ 10x4+ 20 | T28
| $(C_4\times C_2): C_2$ |
| 3 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | * | 1 | x8+ 4x7+ 2x4+ 28 | T28
| $(C_4\times C_2): C_2$ |
| 3 | * | x4- 20
|
| 20 | 4 | 2 | * | 1 | x8+ 4x7+ 10x4+ 28 | T28
| $(C_4\times C_2): C_2$ |
| 3 | * | x4- 20
|
| 20 | 4 | 2 | * | 1 | x8+ 8x7+ 44 | T28
| $(C_4\times C_2): C_2$ |
| 3 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | * | 1 | x8+ 8x7+ 12 | T28
| $(C_4\times C_2): C_2$ |
| 3 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | * | -1 | x8+ 8x6+ 16x3+ 12 | T28
| $(C_4\times C_2): C_2$ |
| 3 | * | x4- 20
|
| 20 | 4 | 2 | -1 | i | x8+ 10x4+ 8x3+ 20 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | -1 | -i | x8+ 8x6+ 10x4+ 8x3+ 28 | T31
| $C_2^4:C_2$ |
| 51/16 | *, 2, 2* | x4- 6x2+ 4
|
| 20 | 4 | 2 | -1 | i | x8+ 10x4+ 8x3+ 12 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 20
|
| 20 | 4 | 2 | -1 | i | x8+ 40x6+ 240 | T31
| $C_2^4:C_2$ |
| 51/16 | *, 2, 2* | x4- 6x2+ 4
|
| 20 | 4 | 2 | -1 | -i | x8+ 24x6+ 240 | T31
| $C_2^4:C_2$ |
| 51/16 | *, 2, 2* | x4- 6x2+ 4
|
| 20 | 4 | 2 | -1 | -i | x8+ 24x6+ 112 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | -1 | -i | x8+ 40x6+ 112 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | -1 | -i | x8+ 8x6+ 240 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 20
|
| 20 | 4 | 2 | -1 | -i | x8+ 56x6+ 64x5+ 240 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 20
|
| 20 | 4 | 2 | -1 | i | x8+ 2x4+ 8x3+ 28 | T31
| $C_2^4:C_2$ |
| 51/16 | *, 2, 2* | x4- 6x2+ 4
|
| 20 | 4 | 2 | -1 | i | x8+ 2x4+ 8x3+ 20 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | -1 | i | x8+ 24x6+ 496 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 51/16 | * | x4+ 2x2+ 20
|
| 20 | 4 | 2 | -1 | i | x8+ 8x6+ 112 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4- 20
|
| 20 | 4 | 2 | -1 | i | x8+ 10x4+ 8x3+ 4 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4- 20
|
| 20 | 4 | 2 | -1 | -i | x8+ 12x6+ 6x4+ 8x3+ 28 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4- 20
|
| 20 | 4 | 2 | -1 | -i | x8+ 8x5+ 10x4+ 8x3+ 16x+ 4 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4- 20
|
| 20 | 4 | 2 | -* | -i | x8+ 14x4+ 8x3+ 20 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4- 20
|
| 20 | 4 | 2 | -* | i | x8+ 4x6+ 10x4+ 8x3+ 4 | T31
| $C_2^4:C_2$ |
| 51/16 | *, -2, -2* | x4- 2x2+ 4
|
| 20 | 4 | 2 | -* | -i | x8+ 6x4+ 8x3+ 20 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4- 20
|
| 20 | 4 | 2 | -* | -i | x8+ 12x6+ 2x4+ 8x3+ 4 | T31
| $C_2^4:C_2$ |
| 51/16 | *, -2, -2* | x4- 2x2+ 4
|
| 20 | 4 | 2 | -* | i | x8+ 4x7+ 8x3+ 44 | T31
| $C_2^4:C_2$ |
| 51/16 | *, -2, -2* | x4- 2x2+ 4
|
| 20 | 4 | 2 | -* | i | x8+ 16x7+ 8x6+ 240 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4- 20
|
| 20 | 4 | 2 | -* | i | x8+ 12x7+ 24x6+ 24x4+ 8x3+ 32x2+ 28 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 51/16 | * | x4- 2x2+ 20
|
| 20 | 4 | 2 | -* | i | x8+ 12x7+ 24x4+ 8x3+ 48x2+ 60 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 51/16 | * | x4- 2x2+ 20
|
| 20 | 4 | 2 | -* | -i | x8+ 6x4+ 8x3+ 28 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 51/16 | * | x4- 2x2+ 20
|
| 20 | 4 | 2 | -* | -i | x8+ 6x4+ 8x3+ 12 | T31
| $C_2^4:C_2$ |
| 51/16 | *, -2, -2* | x4- 2x2+ 4
|
| 20 | 4 | 2 | -* | i | x8+ 4x7+ 14x4+ 8x3+ 16x2+ 20 | T26
| $C_4^2:C_2$ |
| 51/16 | * | x4- 20
|
| 20 | 4 | 2 | -* | -i | x8+ 4x7+ 4x6+ 14x4+ 8x3+ 20 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 51/16 | * | x4- 2x2+ 20
|
| 20 | 4 | 2 | -* | -i | x8+ 6x4+ 8x3+ 4 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | -* | i | x8+ 8x5+ 6x4+ 8x3+ 4 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | -* | -i | x8+ 14x4+ 8x3+ 4 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2- 4
|
| 20 | 4 | 2 | -* | i | x8+ 8x5+ 14x4+ 8x3+ 4 | T30
| $C_4^2:C_2$ |
| 51/16 | * | x4+ 2x2- 4
|
| 20 | 8 | 1 | 1 | 1 | x8+ 4x5+ 2x4+ 2 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 5/2 | -1, -2, 2 | x4+ 6x2+ 1
|
| 20 | 8 | 1 | 1 | 1 | x8+ 4x5+ 6x4+ 14 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 5/2 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x6+ 4x5+ 6x4+ 2 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 5/2 | -1, -2, 2 | x4+ 6x2+ 1
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x6+ 4x5+ 6x4+ 10 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 5/2 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x6+ 4x5+ 2x4+ 6 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 5/2 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 20 | 8 | 1 | 1 | -1 | x8+ 8x6+ 64x+ 16 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 5/2 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 20 | 8 | 1 | 1 | 1 | x8+ 4x5+ 2x4+ 10 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 5/2 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 20 | 8 | 1 | 1 | 1 | x8+ 4x5+ 6x4+ 6 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 5/2 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x6+ 4x5+ 6x4+ 6 | $((C_4\times C_2):C_2):C_2$
| $C_4\times C_2$
|
| 5/2 | -* | x4+ 2x2+ 4x+ 6
|
| 20 | 8 | 1 | 1 | 1 | x8+ 4x5+ 2x4+ 6 | $((C_4\times C_2):C_2):C_2$
| $C_4\times C_2$
|
| 5/2 | -* | x4+ 2x2+ 4x+ 6
|
| 20 | 8 | 1 | 1 | -1 | x8+ 8x6+ 16x5+ 80 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$
|
| 5/2 | -1 | x4+ 6x2+ 4x+ 2
|
| 20 | 8 | 1 | 1 | 1 | x8+ 4x5+ 6x4+ 2 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$
|
| 5/2 | -1 | x4+ 6x2+ 4x+ 2
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x5+ 4x2+ 10 | $S_4\times C_2$
| $A_4\times C_2$
|
| 31/12 | -2* | x4+ 4x2+ 4x+ 2
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x5+ 4x2+ 2 | $S_4\times C_2$
| $A_4\times C_2$
|
| 31/12 | -2 | x4+ 4x2+ 4x+ 2
|
| 20 | 8 | 1 | 1 | -1 | x8+ 24x6+ 20x4+ 36 | $S_4\times C_2$
| $A_4\times C_2$
|
| 31/12 | -2* | x4+ 4x+ 2
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x5+ 4x2+ 14 | $S_4\times C_2$
| $A_4\times C_2$
|
| 31/12 | 2 | x4+ 4x2+ 4x+ 2
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x5+ 4x4+ 4x2+ 2 | $S_4\times C_2$
| $A_4\times C_2$
|
| 31/12 | 2 | x4+ 4x+ 2
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x5+ 4x4+ 4x2+ 10 | $S_4\times C_2$
| $A_4\times C_2$
|
| 31/12 | 2* | x4+ 4x+ 2
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x5+ 4x2+ 6 | $S_4\times C_2$
| $A_4\times C_2$
|
| 31/12 | 2* | x4+ 4x2+ 4x+ 2
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x7+ 4x5+ 4x4+ 4x2+ 2 | $S_4\times C_2$
| $A_4\times C_2$
|
| 31/12 | -2 | x4+ 4x+ 2
|
| 20 | 8 | 1 | 1 | 1 | x8+ 4x5+ 6 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 73/28 | |
|
| 20 | 8 | 1 | 1 | 1 | x8+ 4x5+ 4x4+ 6 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 73/28 | |
|
| 20 | 8 | 1 | 1 | 1 | x8+ 4x5+ 2 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 73/28 | |
|
| 20 | 8 | 1 | 1 | 1 | x8+ 4x5+ 4x4+ 2 | $C_2^3:(C_7:C_3)$
| $C_2^3:C_7$
|
| 73/28 | |
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x5+ 2x4+ 4x2+ 6 | $(C_2^4:C_3):C_2$
| T18
|
| 43/16 | -* |
|
| 20 | 8 | 1 | 1 | 1 | x8+ 8x7+ 80 | $(C_2^4:C_3):C_2$
| T18
|
| 43/16 | -* |
|
| 20 | 8 | 1 | 1 | 1 | x8+ 8x7+ 16 | $(C_2^4:C_3):C_2$
| T18
|
| 43/16 | -1 |
|
| 20 | 8 | 1 | 1 | -1 | x8+ 4x5+ 2x4+ 4x2+ 2 | $(C_2^4:C_3):C_2$
| T18
|
| 43/16 | -1 |
|
| 20 | 8 | 1 | 1 | 1 | x8+ 16x5+ 52 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
|
| 20 | 8 | 1 | 1 | 1 | x8+ 16x2+ 4 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
|
| 20 | 8 | 1 | 1 | -1 | x8+ 6x6+ 4x5+ 6 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
|
| 20 | 8 | 1 | 1 | -1 | x8+ 8x6+ 4 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
|
| 20 | 8 | 1 | 1 | -1 | x8+ 8x6+ 100 | T18
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
x4+ 6x2+ 2
x4+ 6x2+ 10
|
| 20 | 8 | 1 | 1 | 1 | x8+ 16x5+ 20 | T18
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
x4- 2x2- 2
x4- 2x2+ 6
|
| 20 | 8 | 1 | 1 | 1 | x8+ 16x2+ 100 | T18
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
x4- 2x2+ 2
x4+ 6x2+ 10
|
| 20 | 8 | 1 | 1 | -1 | x8+ 6x6+ 4x5+ 12x2+ 6 | T18
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
x4+ 2x2- 2
x4- 2x2+ 6
|
| 20 | 8 | 1 | 1 | -1 | x8+ 8x6+ 36 | T18
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
x4- 2x2+ 2
x4+ 2x2+ 10
|
| 20 | 8 | 1 | 1 | 1 | x8+ 16x2+ 36 | T18
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
x4+ 6x2+ 2
x4+ 2x2+ 10
|
| 20 | 8 | 1 | 1 | -1 | x8+ 2x6+ 4x5+ 12x4+ 12x2+ 6 | T18
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
x4- 2x2- 2
x4+ 2x2+ 6
|
| 20 | 8 | 1 | 1 | 1 | x8+ 16x5+ 84 | T18
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
x4+ 2x2- 2
x4+ 2x2+ 6
|
| 20 | 8 | 1 | * | -1 | x8+ 4x7+ 6x6+ 4x5+ 2 | $(C_8\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
|
| 20 | 8 | 1 | * | 1 | x8+ 52 | $(C_8\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
|
| 20 | 8 | 1 | * | 1 | x8+ 20 | $(C_8\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
|
| 20 | 8 | 1 | * | -1 | x8+ 4x6+ 24x2+ 20 | $(C_8\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
|
| 20 | 8 | 1 | * | 1 | x8+ 8x4+ 20 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
|
| 20 | 8 | 1 | * | 1 | x8+ 8x4+ 52 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
|
| 20 | 8 | 1 | * | 1 | x8+ 8x4+ 116 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
|
| 20 | 8 | 1 | * | -1 | x8+ 4x7+ 8x2+ 56 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
|
| 20 | 8 | 1 | * | -1 | x8+ 2x6+ 4x5+ 8x3+ 14 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
|
| 20 | 8 | 1 | * | -1 | x8+ 4x7+ 2x6+ 4x5+ 6 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
|
| 20 | 8 | 1 | * | 1 | x8+ 8x4+ 84 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -1 | x4+ 2x3+ 2
|
| 20 | 8 | 1 | * | -1 | x8+ 2x6+ 4x5+ 12x2+ 6 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 23/8 | -* | x4+ 2x3+ 6
|
| 20 | 8 | 1 | -1 | i | x8+ 4x6+ 28 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -1 | -i | x8+ 12x6+ 60 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -1 | i | x8+ 4x6+ 60 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -1 | -i | x8+ 12x6+ 28 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -1 | i | x8+ 24x2+ 60 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -1 | -i | x8+ 8x2+ 28 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -1 | i | x8+ 24x2+ 28 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -1 | -i | x8+ 8x2+ 60 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -* | i | x8+ 20x6+ 12 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -* | i | x8+ 8x2+ 12 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -* | -i | x8+ 24x2+ 12 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -* | -i | x8+ 12x6+ 12 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -* | i | x8+ 4x6+ 12 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -* | -i | x8+ 28x6+ 12 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -* | i | x8+ 40x2+ 12 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
| 20 | 8 | 1 | -* | -i | x8+ 56x2+ 12 | T38
| T31
|
| 99/32 | | x4+ 2x3+ 2x2+ 2
|
|
|
| 21 | 8 | 1 | 2 | 1 | x8+ 2x6+ 4x2+ 2 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2 | 1 | x8+ 14x6+ 12x4+ 2 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2 | -1 | x8+ 10x6+ 2 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2 | -1 | x8+ 6x6+ 8x4+ 2 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2 | 1 | x8+ 2x6+ 2 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2 | -1 | x8+ 10x6+ 12x4+ 2 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2 | -1 | x8+ 8x2+ 8 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2 | 1 | x8+ 24x2+ 8 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2 | 1 | x8+ 14x6+ 10x4+ 2 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2 | -1 | x8+ 6x6+ 10x4+ 2 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2 | 1 | x8+ 14x6+ 14x4+ 2 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2 | 1 | x8+ 2x6+ 10x4+ 2 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2 | 1 | x8+ 14x6+ 6x4+ 2 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2 | -1 | x8+ 10x6+ 14x4+ 2 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2 | -1 | x8+ 6x6+ 14x4+ 2 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2 | -1 | x8+ 6x6+ 2x4+ 2 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2* | 1 | x8+ 4x6+ 160 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2* | -1 | x8+ 8x6+ 56x2+ 40 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2* | -1 | x8+ 6x6+ 10 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2* | -1 | x8+ 8x2+ 40 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2* | 1 | x8+ 14x6+ 12x4+ 10 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2* | 1 | x8+ 2x6+ 4x2+ 10 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2* | 1 | x8+ 2x6+ 10 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2* | -1 | x8+ 6x6+ 8x4+ 10 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x3+ 2
|
| 21 | 8 | 1 | 2* | -1 | x8+ 10x6+ 10x4+ 8x2+ 10 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2* | 1 | x8+ 2x6+ 14x4+ 10 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2* | 1 | x8+ 14x6+ 2x4+ 10 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2* | -1 | x8+ 10x6+ 6x4+ 10 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2* | -1 | x8+ 10x6+ 14x4+ 10 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2* | 1 | x8+ 2x6+ 6x4+ 10 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2* | -1 | x8+ 6x6+ 2x4+ 10 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | 2* | 1 | x8+ 2x6+ 2x4+ 10 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2 | -i | x8+ 10x6+ 12x2+ 14 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2 | i | x8+ 2x6+ 8x4+ 14 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2 | i | x8+ 4x7+ 14x6+ 14 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2 | -i | x8+ 14x6+ 14 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2 | i | x8+ 8x2+ 56 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2 | -i | x8+ 56x2+ 56 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2 | -i | x8+ 4x7+ 6x6+ 14 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2 | i | x8+ 2x6+ 14 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2 | -i | x8+ 10x6+ 2x4+ 14 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2 | i | x8+ 6x6+ 6x4+ 14 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2 | -i | x8+ 10x6+ 6x4+ 14 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2 | i | x8+ 6x6+ 10x4+ 14 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2 | -i | x8+ 14x6+ 6x4+ 14 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2 | i | x8+ 6x6+ 2x4+ 14 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2 | -i | x8+ 14x6+ 2x4+ 14 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2 | i | x8+ 6x6+ 14x4+ 14 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2* | -i | x8+ 56x2+ 24 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2* | i | x8+ 4x7+ 2x6+ 14 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2* | i | x8+ 2x6+ 8x5+ 6 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2* | -i | x8+ 10x6+ 6 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2* | i | x8+ 8x2+ 24 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2* | -i | x8+ 14x6+ 4x2+ 6 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2* | -i | x8+ 4x7+ 6x6+ 6 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2* | i | x8+ 2x6+ 6 | T35
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x3+ 6
|
| 21 | 8 | 1 | -2* | i | x8+ 2x6+ 6x4+ 6 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2* | i | x8+ 2x6+ 2x4+ 6 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2* | -i | x8+ 4x4+ 24x2+ 24 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2* | i | x8+ 2x6+ 14x4+ 6 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2* | -i | x8+ 14x6+ 2x4+ 6 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2* | -i | x8+ 10x6+ 14x4+ 6 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2* | i | x8+ 6x6+ 2x4+ 6 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
| 21 | 8 | 1 | -2* | -i | x8+ 14x6+ 14x4+ 6 | T38
| T31
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 3 | | |
| 111/32 | | x4+ 2x3+ 2x2+ 2
|
|
|
| 22 | 4 | 2 | 1 | 1 | x8+ 8x5+ 6x4+ 16x3+ 8x2+ 12 | $D_4$
| $C_4$ |
| 11/4 | *, -2, -2* | x4- 2x2+ 4
x4+ 4x2+ 14
x4+ 12x2+ 6
|
| 22 | 4 | 2 | 1 | -1 | x8+ 10x4+ 16x+ 4 | $C_4\times C_2$
| $C_4$ |
| 11/4 | *, 2, 2* | x4- 6x2+ 4
x4+ 12x2+ 18
x4+ 12x2+ 2
|
| 22 | 4 | 2 | 1 | 1 | x8+ 8x6+ 6x4+ 16x2+ 16x+ 4 | $Q_8$
| $C_4$ |
| 11/4 | *, -2, -2* | x4- 2x2+ 4
|
| 22 | 4 | 2 | 1 | 1 | x8+ 8x7+ 8x5+ 6x4+ 24x2+ 12 | $Q_8$
| $C_4$ |
| 11/4 | *, -2, -2* | x4- 2x2+ 4
|
| 22 | 4 | 2 | 1 | -1 | x8+ 10x4+ 16x+ 36 | $C_4\times C_2$
| $C_4$ |
| 11/4 | *, 2, 2* | x4- 6x2+ 4
x4+ 8x+ 6
x4+ 4x2+ 10
|
| 22 | 4 | 2 | 1 | -1 | x8+ 4x6+ 6x4+ 16x3+ 24x2+ 36 | $C_4\times C_2$
| $C_4$ |
| 11/4 | *, 2, 2* | x4- 6x2+ 4
x4+ 12x2+ 10
x4+ 8x2+ 8x+ 22
|
| 22 | 4 | 2 | 1 | -1 | x8+ 2x4+ 16x+ 4 | $C_4\times C_2$
| $C_4$ |
| 11/4 | *, 2, 2* | x4- 6x2+ 4
x4+ 4x2+ 18
x4+ 8x+ 14
|
| 22 | 4 | 2 | 1 | 1 | x8+ 12x6+ 10x4+ 8x2+ 36 | $D_4$
| $C_4$ |
| 11/4 | *, -2, -2* | x4- 2x2+ 4
x4+ 8x+ 10
x4+ 4x2+ 6
|
| 22 | 4 | 2 | 1 | 1 | x8+ 2x4+ 4 | $D_4\times C_2$
| $D_4$ |
| 3 | *, 2, 2* | x4- 6x2+ 4
x4+ 30
x4+ 14
|
| 22 | 4 | 2 | 1 | -1 | x8+ 12x4+ 68 | $(C_4\times C_2):C_2$
| $C_4\times C_2$ |
| 3 | *, -2, -2* | x4- 2x2+ 4
|
| 22 | 4 | 2 | 1 | -1 | x8+ 4x6+ 2x4+ 8x2+ 36 | $(C_4\times C_2):C_2$
| $C_4\times C_2$ |
| 3 | *, -2, -2* | x4- 2x2+ 4
|
| 22 | 4 | 2 | 1 | 1 | x8+ 10x4+ 4 | $(C_4\times C_2):C_2$
| $D_4$ |
| 3 | *, 2, 2* | x4- 6x2+ 4
|
| 22 | 4 | 2 | 1 | 1 | x8+ 52x4+ 4 | $(C_4\times C_2):C_2$
| $C_4\times C_2$ |
| 3 | *, 2, 2* | x4- 6x2+ 4
|
| 22 | 4 | 2 | 1 | 1 | x8+ 10x4+ 36 | $D_4\times C_2$
| $D_4$ |
| 3 | *, 2, 2* | x4- 6x2+ 4
x4+ 6
x4+ 22
|
| 22 | 4 | 2 | 1 | 1 | x8+ 2x4+ 36 | $(C_4\times C_2):C_2$
| $D_4$ |
| 3 | *, 2, 2* | x4- 6x2+ 4
|
| 22 | 4 | 2 | 1 | -1 | x8+ 14x4+ 4 | $D_4\times C_2$
| $D_4$ |
| 3 | *, -2, -2* | x4- 2x2+ 4
x4+ 2
x4+ 18
|
| 22 | 4 | 2 | 1 | 1 | x8+ 2x4+ 16x3+ 16x+ 4 | $(C_4\times C_2):C_2$
| $C_4\times C_2$ |
| 3 | *, 2, 2* | x4- 6x2+ 4
|
| 22 | 4 | 2 | 1 | -1 | x8+ 14x4+ 36 | $(C_4\times C_2):C_2$
| $D_4$ |
| 3 | *, -2, -2* | x4- 2x2+ 4
|
| 22 | 4 | 2 | 1 | -1 | x8+ 6x4+ 36 | $D_4\times C_2$
| $D_4$ |
| 3 | *, -2, -2* | x4- 2x2+ 4
x4+ 26
x4+ 10
|
| 22 | 4 | 2 | 1 | -1 | x8+ 6x4+ 4 | $(C_4\times C_2):C_2$
| $D_4$ |
| 3 | *, -2, -2* | x4- 2x2+ 4
|
| 22 | 4 | 2 | 1 | -1 | x8+ 4x6+ 6x4+ 16x+ 52 | T29
| $C_2^4:C_2$ |
| 55/16 | * | x4- 20
|
| 22 | 4 | 2 | 1 | -1 | x8+ 8x6+ 6x4+ 24x2+ 4 | T29
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | 1 | 1 | x8+ 14x4+ 8x2+ 4 | T29
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | 1 | -1 | x8+ 8x5+ 2x4+ 60 | T29
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | 1 | 1 | x8+ 8x7+ 12x6+ 2x4+ 4 | T29
| $C_2^4:C_2$ |
| 55/16 | * | x4- 20
|
| 22 | 4 | 2 | 1 | 1 | x8+ 16x7+ 4x6+ 36x4+ 56x2+ 20 | T29
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | 1 | 1 | x8+ 4x6+ 2x4+ 36 | T29
| $C_2^4:C_2$ |
| 55/16 | * | x4- 20
|
| 22 | 4 | 2 | 1 | -1 | x8+ 2x4+ 8x2+ 4 | T29
| $C_2^4:C_2$ |
| 55/16 | * | x4- 20
|
| 22 | 4 | 2 | * | 1 | x8+ 4x6+ 24x5+ 8x2+ 48x+ 12 | $C_{8}$
| $C_4$ |
| 11/4 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | * | 1 | x8+ 2x4+ 16x3+ 16x+ 52 | $C_{8}$
| $C_4$ |
| 11/4 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | * | 1 | x8+ 12x6+ 6x4+ 8x2+ 52 | $C_{8}$
| $C_4$ |
| 11/4 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | * | 1 | x8+ 8x7+ 2x4+ 16x3+ 16x+ 20 | $C_{8}$
| $C_4$ |
| 11/4 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | * | -1 | x8+ 16x6+ 20x4+ 116 | $C_8:C_2$
| $C_4$ |
| 11/4 | * | x4- 2x2+ 20
|
| 22 | 4 | 2 | * | -1 | x8+ 4x6+ 10x4+ 8x2+ 20 | $C_8:C_2$
| $C_4$ |
| 11/4 | * | x4- 2x2+ 20
|
| 22 | 4 | 2 | * | -1 | x8+ 4x6+ 6x4+ 8x2+ 52 | $C_8:C_2$
| $C_4\times C_2$ |
| 3 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | * | 1 | x8+ 6x4+ 16x+ 52 | $C_8:C_2$
| $C_4\times C_2$ |
| 3 | * | x4- 2x2+ 20
|
| 22 | 4 | 2 | * | 1 | x8+ 12x6+ 2x4+ 8x2+ 52 | $C_8:C_2$
| $C_4\times C_2$ |
| 3 | * | x4- 2x2+ 20
|
| 22 | 4 | 2 | * | -1 | x8+ 2x4+ 16x+ 52 | $C_8:C_2$
| $C_4\times C_2$ |
| 3 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | * | 1 | x8+ 2x4+ 20 | $(C_8:C_2):C_2$
| $D_4\times C_2$ |
| 25/8 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | * | -1 | x8+ 6x4+ 20 | $(C_8:C_2):C_2$
| $D_4\times C_2$ |
| 25/8 | * | x4- 2x2+ 20
|
| 22 | 4 | 2 | * | -1 | x8+ 6x4+ 52 | $(C_8:C_2):C_2$
| $D_4\times C_2$ |
| 25/8 | * | x4- 2x2+ 20
|
| 22 | 4 | 2 | * | 1 | x8+ 2x4+ 52 | $(C_8:C_2):C_2$
| $D_4\times C_2$ |
| 25/8 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | * | -1 | x8+ 2x4+ 8x2+ 52 | T28
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | * | -1 | x8+ 8x5+ 2x4+ 12 | T28
| $C_2^4:C_2$ |
| 55/16 | * | x4- 20
|
| 22 | 4 | 2 | * | 1 | x8+ 4x6+ 6x4+ 20 | T28
| $C_2^4:C_2$ |
| 55/16 | * | x4- 20
|
| 22 | 4 | 2 | * | -1 | x8+ 8x5+ 2x4+ 44 | T28
| $C_2^4:C_2$ |
| 55/16 | * | x4- 20
|
| 22 | 4 | 2 | * | 1 | x8+ 8x5+ 6x4+ 60 | T28
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | * | -1 | x8+ 12x6+ 2x4+ 20 | T28
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | * | 1 | x8+ 4x6+ 6x4+ 52 | T28
| $C_2^4:C_2$ |
| 55/16 | * | x4- 20
|
| 22 | 4 | 2 | * | 1 | x8+ 4x6+ 32x5+ 52x4+ 24x2+ 52 | T28
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | -1 | -i | x8+ 14x4+ 60 | $D_8$
| $D_4$ |
| 3 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | -1 | -i | x8+ 2x4+ 60 | $D_8$
| $D_4$ |
| 3 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | -1 | -i | x8+ 2x4+ 28 | $QD_{16}$
| $D_4$ |
| 3 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | -1 | -i | x8+ 10x4+ 28 | $QD_{16}$
| $D_4$ |
| 3 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | -1 | i | x8+ 8x5+ 2x4+ 8x2+ 4 | T30
| $C_4^2:C_2$ |
| 13/4 | * | x4- 20
|
| 22 | 4 | 2 | -1 | -i | x8+ 16x5+ 12 | T30
| $C_4^2:C_2$ |
| 13/4 | * | x4- 20
|
| 22 | 4 | 2 | -1 | -i | x8+ 32x+ 44 | T30
| $C_4^2:C_2$ |
| 13/4 | * | x4- 20
|
| 22 | 4 | 2 | -1 | i | x8+ 8x6+ 8x5+ 2x4+ 16x3+ 8x2+ 4 | T30
| $C_4^2:C_2$ |
| 13/4 | * | x4- 20
|
| 22 | 4 | 2 | -1 | -i | x8+ 4x6+ 2x4+ 28 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 55/16 | * | x4- 2x2+ 20
|
| 22 | 4 | 2 | -1 | -i | x8+ 8x5+ 6x4+ 20 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 55/16 | * | x4- 2x2+ 20
|
| 22 | 4 | 2 | -1 | i | x8+ 8x7+ 12x6+ 8x5+ 2x4+ 8x2+ 20 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 55/16 | * | x4- 2x2+ 20
|
| 22 | 4 | 2 | -1 | -i | x8+ 8x5+ 10x4+ 4 | T31
| $C_2^4:C_2$ |
| 55/16 | *, 2, 2* | x4- 6x2+ 4
|
| 22 | 4 | 2 | -1 | -i | x8+ 2x4+ 8x2+ 60 | T31
| $C_2^4:C_2$ |
| 55/16 | *, 2, 2* | x4- 6x2+ 4
|
| 22 | 4 | 2 | -1 | i | x8+ 4x6+ 6x4+ 28 | T31
| $C_2^4:C_2$ |
| 55/16 | *, 2, 2* | x4- 6x2+ 4
|
| 22 | 4 | 2 | -1 | i | x8+ 4x6+ 6x4+ 60 | T31
| $C_2^4:C_2$ |
| 55/16 | *, 2, 2* | x4- 6x2+ 4
|
| 22 | 4 | 2 | -1 | i | x8+ 12x6+ 2x4+ 28 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 55/16 | * | x4- 2x2+ 20
|
| 22 | 4 | 2 | -* | -i | x8+ 12 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 25/8 | * | x4- 20
|
| 22 | 4 | 2 | -* | -i | x8+ 2x4+ 12 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 25/8 | * | x4- 20
|
| 22 | 4 | 2 | -* | -i | x8+ 6x4+ 44 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 25/8 | * | x4- 20
|
| 22 | 4 | 2 | -* | -i | x8+ 192 | $(C_8\times C_2):C_2$
| $D_4\times C_2$ |
| 25/8 | * | x4- 20
|
| 22 | 4 | 2 | -* | i | x8+ 24x6+ 44 | T30
| $C_4^2$ |
| 13/4 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | -* | -i | x8+ 16x2+ 44 | T30
| $C_4^2$ |
| 13/4 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | -* | i | x8+ 8x6+ 44 | T30
| $C_4^2$ |
| 13/4 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | -* | -i | x8+ 16x2+ 12 | T30
| $C_4^2$ |
| 13/4 | * | x4+ 2x2- 4
|
| 22 | 4 | 2 | -* | i | x8+ 12x6+ 8x2+ 44 | T31
| $C_2^4:C_2$ |
| 55/16 | *, -2, -2* | x4- 2x2+ 4
|
| 22 | 4 | 2 | -* | -i | x8+ 8x5+ 10x4+ 20 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | -* | -i | x8+ 6x4+ 8x2+ 44 | T31
| $C_2^4:C_2$ |
| 55/16 | *, -2, -2* | x4- 2x2+ 4
|
| 22 | 4 | 2 | -* | i | x8+ 4x6+ 6x4+ 12 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | -* | -i | x8+ 2x4+ 8x2+ 44 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | -* | i | x8+ 2x4+ 24x2+ 44 | $((C_8\times C_2):C_2):C_2$
| $C_2^4:C_2$ |
| 55/16 | * | x4+ 2x2+ 20
|
| 22 | 4 | 2 | -* | i | x8+ 12x6+ 10x4+ 12 | T31
| $C_2^4:C_2$ |
| 55/16 | *, -2, -2* | x4- 2x2+ 4
|
| 22 | 4 | 2 | -* | -i | x8+ 14x4+ 8x2+ 44 | T31
| $C_2^4:C_2$ |
| 55/16 | *, -2, -2* | x4- 2x2+ 4
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 2x4+ 4x2+ 14 | $D_4$
| $D_4$
|
| 11/4 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
x4+ 2x2+ 6
x4+ 6x2+ 3
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 10x4+ 4x2+ 14 | $D_4$
| $D_4$
|
| 11/4 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
x4- 2x2+ 6
x4- 6x2+ 3
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 10x4+ 4x2+ 6 | $D_4$
| $D_4$
|
| 11/4 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
x4- 2x2- 2
x4+ 2x2+ 3
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 14x4+ 12x2+ 10 | $D_4$
| $D_4$
|
| 11/4 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
x4+ 6x2+ 10
x4+ 2x2- 9
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 6x4+ 12x2+ 2 | $D_4$
| $D_4$
|
| 11/4 | -1, -2, 2 | x4+ 6x2+ 1
x4- 2x2+ 2
x4+ 2x2- 1
|
| 22 | 8 | 1 | 1 | 1 | x8+ 152x4+ 16 | $D_4$
| $D_4$
|
| 11/4 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
x4+ 2x2+ 10
x4+ 6x2- 1
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 2x4+ 4x2+ 6 | $D_4$
| $D_4$
|
| 11/4 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
x4+ 2x2- 2
x4- 2x2+ 3
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 14x4+ 12x2+ 2 | $D_4$
| $D_4$
|
| 11/4 | -1, -2, 2 | x4+ 6x2+ 1
x4+ 6x2+ 2
x4+ 6x2- 9
|
| 22 | 8 | 1 | 1 | -1 | x8+ 56x4+ 144 | $(C_4\times C_2):C_2$
| $D_4$
|
| 11/4 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 6x4+ 12x2+ 8x+ 10 | $(C_4\times C_2):C_2$
| $D_4$
|
| 11/4 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 22 | 8 | 1 | 1 | 1 | x8+ 56x4+ 400 | $D_4\times C_2$
| $D_4$
|
| 11/4 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
x4+ 6x2+ 3
x4- 6x2+ 3
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 4x6+ 6x4+ 8x3+ 12x2+ 14 | $(C_4\times C_2):C_2$
| $D_4$
|
| 11/4 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 22 | 8 | 1 | 1 | 1 | x8+ 184x4+ 400 | $D_4\times C_2$
| $D_4$
|
| 11/4 | -1, -2, 2 | x4+ 6x2+ 1
x4+ 2x2+ 3
x4- 2x2+ 3
|
| 22 | 8 | 1 | 1 | -1 | x8+ 24x4+ 272 | $D_4\times C_2$
| $D_4$
|
| 11/4 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
x4+ 2x2+ 6
x4- 2x2+ 6
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 6x4+ 4x2+ 10 | $D_4\times C_2$
| $D_4$
|
| 11/4 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
x4- 2x2+ 2
x4+ 6x2+ 2
|
| 22 | 8 | 1 | 1 | -1 | x8+ 24x4+ 784 | $D_4\times C_2$
| $D_4$
|
| 11/4 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
x4+ 2x2- 2
x4- 2x2- 2
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 4x6+ 6x4+ 12x2+ 14 | $D_4\times C_2$
| $D_4$
|
| 11/4 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
x4+ 6x2- 9
x4+ 2x2- 1
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 4x6+ 2x4+ 12x2+ 2 | $(C_4\times C_2):C_2$
| $D_4$
|
| 11/4 | -1, -2, 2 | x4+ 6x2+ 1
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 4x6+ 6x4+ 8x3+ 4x2+ 6 | $D_4\times C_2$
| $D_4$
|
| 11/4 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
x4+ 6x2- 1
x4+ 2x2- 9
|
| 22 | 8 | 1 | 1 | -1 | x8+ 8x7+ 16x5+ 144 | $D_4\times C_2$
| $D_4$
|
| 11/4 | -1, -2, 2 | x4+ 6x2+ 1
x4+ 6x2+ 10
x4+ 2x2+ 10
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 4x6+ 2x4+ 12x2+ 6 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x2+ 4x+ 6
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 4x6+ 2x4+ 8x3+ 12x2+ 6 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x2+ 4x+ 6
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 4x6+ 6x4+ 12x2+ 2 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 6x2+ 4x+ 2
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 2x4+ 8x3+ 12x2+ 8x+ 2 | $((C_4\times C_2):C_2):C_2$
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 6x2+ 4x+ 2
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 2x4+ 4x2+ 2 | T18
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 6x2+ 4x+ 2
x4- 2x2+ 2
x4+ 2x2+ 10
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 14x4+ 12x2+ 6 | T18
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x2+ 4x+ 6
x4+ 2x2- 2
x4+ 2x2+ 6
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 6x4+ 12x2+ 6 | T18
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x2+ 4x+ 6
x4- 2x2- 2
x4- 2x2+ 6
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 2x4+ 12x2+ 10 | T18
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 6x2+ 4x+ 2
x4+ 6x2+ 2
x4+ 2x2+ 10
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 10x4+ 12x2+ 10 | T18
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 6x2+ 4x+ 2
x4- 2x2+ 2
x4+ 6x2+ 10
|
| 22 | 8 | 1 | 1 | -1 | x8+ 8x7+ 48x5+ 80 | T18
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x2+ 4x+ 6
x4- 2x2- 2
x4+ 2x2+ 6
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 10x4+ 4x2+ 2 | T18
| $D_4\times C_2$
|
| 23/8 | -1 | x4+ 6x2+ 4x+ 2
x4+ 6x2+ 2
x4+ 6x2+ 10
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 6x4+ 4x2+ 14 | T18
| $D_4\times C_2$
|
| 23/8 | -* | x4+ 2x2+ 4x+ 6
x4+ 2x2- 2
x4- 2x2+ 6
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 4x6+ 10 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 3, 19/6, 19/6] | 2 | | 3 |
| 139/48 | -2* |
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 2 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 3, 19/6, 19/6] | 2 | | 3 |
| 139/48 | 2 |
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 3, 19/6, 19/6] | 2 | | 3 |
| 139/48 | -2 |
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 4x6+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 3, 19/6, 19/6] | 2 | | 3 |
| 139/48 | 2* |
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 4x6+ 2 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 3, 19/6, 19/6] | 2 | | 3 |
| 139/48 | -2 |
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 4x6+ 14 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 3, 19/6, 19/6] | 2 | | 3 |
| 139/48 | 2 |
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 14 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 3, 19/6, 19/6] | 2 | | 3 |
| 139/48 | -2* |
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 10 | T41
| $(C_2^4:C_3):C_2$
|
| [4/3, 4/3, 3, 19/6, 19/6] | 2 | | 3 |
| 139/48 | 2* |
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 4x6+ 2x4+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [2, 8/3, 8/3, 10/3, 10/3] | 2 | | 3 |
| 37/12 | -* |
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 2x4+ 2 | T41
| $(C_2^4:C_3):C_2$
|
| [2, 8/3, 8/3, 10/3, 10/3] | 2 | | 3 |
| 37/12 | -1 |
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 2x4+ 8x2+ 2 | T41
| $(C_2^4:C_3):C_2$
|
| [2, 8/3, 8/3, 10/3, 10/3] | 2 | | 3 |
| 37/12 | -1 |
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 6x4+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [2, 8/3, 8/3, 10/3, 10/3] | 2 | | 3 |
| 37/12 | -* |
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 6x4+ 2 | T41
| $(C_2^4:C_3):C_2$
|
| [2, 8/3, 8/3, 10/3, 10/3] | 2 | | 3 |
| 37/12 | -1 |
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 4x6+ 2x4+ 2 | T41
| $(C_2^4:C_3):C_2$
|
| [2, 8/3, 8/3, 10/3, 10/3] | 2 | | 3 |
| 37/12 | -1 |
|
| 22 | 8 | 1 | 1 | -1 | x8+ 4x7+ 2x4+ 8x2+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [2, 8/3, 8/3, 10/3, 10/3] | 2 | | 3 |
| 37/12 | -* |
|
| 22 | 8 | 1 | 1 | 1 | x8+ 4x7+ 2x4+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [2, 8/3, 8/3, 10/3, 10/3] | 2 | | 3 |
| 37/12 | -* |
|
| 22 | 8 | 1 | * | 1 | x8+ 12x6+ 8x5+ 56 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 17/6 | | x4+ 4x+ 2
|
| 22 | 8 | 1 | * | 1 | x8+ 4x7+ 12x2+ 14 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 17/6 | | x4+ 4x+ 2
|
| 22 | 8 | 1 | * | 1 | x8+ 4x7+ 4x2+ 10 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 17/6 | | x4+ 4x+ 2
|
| 22 | 8 | 1 | * | 1 | x8+ 4x7+ 4x2+ 2 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 17/6 | | x4+ 4x+ 2
|
| 22 | 8 | 1 | * | 1 | x8+ 4x7+ 4x2+ 6 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 17/6 | | x4+ 4x+ 2
|
| 22 | 8 | 1 | * | 1 | x8+ 4x7+ 4x2+ 14 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 17/6 | | x4+ 4x+ 2
|
| 22 | 8 | 1 | * | 1 | x8+ 4x7+ 12x2+ 2 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 17/6 | | x4+ 4x+ 2
|
| 22 | 8 | 1 | * | 1 | x8+ 4x7+ 12x2+ 10 | $\textrm{GL}_2(3)$
| $\textrm{SL}_2(3)$
|
| 17/6 | | x4+ 4x+ 2
|
| 22 | 8 | 1 | * | -1 | x8+ 4x7+ 4x4+ 4x2+ 14 | T40
| T32
|
| [4/3, 4/3, 8/3, 8/3, 7/2] | 2 | | 3 |
| 139/48 | | x4+ 4x2+ 4x+ 2
|
| 22 | 8 | 1 | * | -1 | x8+ 4x7+ 4x4+ 12x2+ 2 | T40
| T32
|
| [4/3, 4/3, 8/3, 8/3, 7/2] | 2 | | 3 |
| 139/48 | | x4+ 4x2+ 4x+ 2
|
| 22 | 8 | 1 | * | -1 | x8+ 4x7+ 4x4+ 4x2+ 6 | T40
| T32
|
| [4/3, 4/3, 8/3, 8/3, 7/2] | 2 | | 3 |
| 139/48 | | x4+ 4x2+ 4x+ 2
|
| 22 | 8 | 1 | * | -1 | x8+ 4x7+ 4x6+ 4x4+ 4x2+ 2 | T40
| T32
|
| [4/3, 4/3, 8/3, 8/3, 7/2] | 2 | | 3 |
| 139/48 | | x4+ 4x2+ 4x+ 2
|
| 22 | 8 | 1 | * | -1 | x8+ 4x7+ 4x4+ 4x2+ 2 | T40
| T32
|
| [4/3, 4/3, 8/3, 8/3, 7/2] | 2 | | 3 |
| 139/48 | | x4+ 4x2+ 4x+ 2
|
| 22 | 8 | 1 | * | -1 | x8+ 4x7+ 4x4+ 12x2+ 10 | T40
| T32
|
| [4/3, 4/3, 8/3, 8/3, 7/2] | 2 | | 3 |
| 139/48 | | x4+ 4x2+ 4x+ 2
|
| 22 | 8 | 1 | * | -1 | x8+ 4x4+ 16x2+ 116 | T40
| T32
|
| [4/3, 4/3, 8/3, 8/3, 7/2] | 2 | | 3 |
| 139/48 | | x4+ 4x2+ 4x+ 2
|
| 22 | 8 | 1 | * | -1 | x8+ 4x7+ 4x4+ 12x2+ 14 | T40
| T32
|
| [4/3, 4/3, 8/3, 8/3, 7/2] | 2 | | 3 |
| 139/48 | | x4+ 4x2+ 4x+ 2
|
|
|
| 24 | 8 | 1 | 1 | -1 | x8+ 14x4+ 4x2+ 8x+ 22 | $C_4\times C_2$
| $C_4\times C_2$
|
| 3 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
x4+ 4x2+ 10
x4+ 8x2+ 8x+ 22
|
| 24 | 8 | 1 | 1 | -1 | x8+ 14x4+ 4x2+ 8x+ 6 | $C_4\times C_2$
| $C_4\times C_2$
|
| 3 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
x4+ 8x+ 6
x4+ 12x2+ 10
|
| 24 | 8 | 1 | 1 | 1 | x8+ 2x4+ 8x3+ 12x2+ 8x+ 18 | $D_4$
| $D_4$
|
| 3 | -1, -2, 2 | x4+ 6x2+ 1
x4+ 14
x4+ 18
|
| 24 | 8 | 1 | 1 | 1 | x8+ 14x4+ 8x3+ 12x2+ 8x+ 14 | $Q_8$
| $Q_8$
|
| 3 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 24 | 8 | 1 | 1 | 1 | x8- 15 | $C_4\times C_2$
| $C_4\times C_2$
|
| 3 | -1, -2, 2 | x4+ 6x2+ 1
x4+ 12x2+ 18
x4+ 4x2+ 18
|
| 24 | 8 | 1 | 1 | 1 | x8+ 44x4+ 100 | $D_4$
| $D_4$
|
| 3 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
x4+ 6
x4+ 10
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x7+ 12x6+ 10x4+ 8x3+ 4x2+ 8x+ 14 | $C_4\times C_2$
| $C_4\times C_2$
|
| 3 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
x4+ 12x2+ 18
x4+ 8x+ 14
|
| 24 | 8 | 1 | 1 | 1 | x8+ 8x7+ 14x4+ 8x3+ 12x2+ 8x+ 22 | $Q_8$
| $Q_8$
|
| 3 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x7+ 14x4+ 4x2+ 8x+ 30 | $C_4\times C_2$
| $C_4\times C_2$
|
| 3 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
x4+ 4x2+ 18
x4+ 12x2+ 2
|
| 24 | 8 | 1 | 1 | 1 | x8+ 16 | $C_4\times C_2$
| $C_4\times C_2$
|
| 3 | -1, -2, 2 | x4+ 6x2+ 1
x4+ 8x+ 14
x4+ 12x2+ 2
|
| 24 | 8 | 1 | 1 | 1 | x8+ 8x7+ 8x5+ 2x4+ 12x2+ 8x+ 26 | $C_4\times C_2$
| $C_4\times C_2$
|
| 3 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
x4+ 8x+ 6
x4+ 8x2+ 8x+ 22
|
| 24 | 8 | 1 | 1 | 1 | x8+ 14x4+ 8x3+ 12x2+ 8x+ 30 | $Q_8$
| $Q_8$
|
| 3 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 24 | 8 | 1 | 1 | 1 | x8+ 28x4+ 36 | $C_4\times C_2$
| $C_4\times C_2$
|
| 3 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
x4+ 12x2+ 10
x4+ 4x2+ 10
|
| 24 | 8 | 1 | 1 | 1 | x8+ 12x6+ 6x4+ 4x2+ 8x+ 2 | $D_4$
| $D_4$
|
| 3 | -1, -2, 2 | x4+ 6x2+ 1
x4+ 30
x4+ 2
|
| 24 | 8 | 1 | 1 | 1 | x8+ 52x4+ 36 | $D_4$
| $D_4$
|
| 3 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
x4+ 22
x4+ 26
|
| 24 | 8 | 1 | 1 | 1 | x8+ 4x6+ 2x4+ 4x2+ 8x+ 6 | $Q_8$
| $Q_8$
|
| 3 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 24 | 8 | 1 | 1 | -1 | x8+ 16x4+ 16 | $D_4\times C_2$
| $C_4\times C_2$
|
| 3 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
x4+ 12x2+ 6
x4+ 4x2+ 6
|
| 24 | 8 | 1 | 1 | -1 | x8+ 2x4+ 8x3+ 4x2+ 8x+ 10 | $(C_4\times C_2):C_2$
| $Q_8$
|
| 3 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 24 | 8 | 1 | 1 | 1 | x8+ 16x6+ 16 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 3 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 24 | 8 | 1 | 1 | -1 | x8+ 10x4+ 8x3+ 4x2+ 8x+ 2 | $(C_4\times C_2):C_2$
| $Q_8$
|
| 3 | -1, -2, 2 | x4+ 6x2+ 1
|
| 24 | 8 | 1 | 1 | 1 | x8+ 20x4+ 4 | $D_4\times C_2$
| $C_4\times C_2$
|
| 3 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
x4+ 8x+ 10
x4+ 4x2+ 14
|
| 24 | 8 | 1 | 1 | 1 | x8+ 4x4+ 36 | $D_4\times C_2$
| $C_4\times C_2$
|
| 3 | -1, -2, 2 | x4+ 6x2+ 1
x4+ 12x2+ 6
x4+ 4x2+ 6
|
| 24 | 8 | 1 | 1 | -1 | x8+ 44x4+ 68 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 3 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 24 | 8 | 1 | 1 | -1 | x8+ 2x4+ 8x3+ 4x2+ 8x+ 2 | $(C_4\times C_2):C_2$
| $Q_8$
|
| 3 | -1, -2, 2 | x4+ 6x2+ 1
|
| 24 | 8 | 1 | 1 | 1 | x8- 7 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 3 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x7+ 4x6+ 8x5+ 10x4+ 4x2+ 8x+ 14 | $D_4\times C_2$
| $D_4$
|
| 3 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
x4+ 26
x4+ 10
|
| 24 | 8 | 1 | 1 | -1 | x8+ 28x4+ 4 | $D_4\times C_2$
| $D_4$
|
| 3 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
x4+ 2
x4+ 18
|
| 24 | 8 | 1 | 1 | 1 | x8+ 12x6+ 8x4+ 12x2+ 9 | $(C_4\times C_2):C_2$
| $D_4$
|
| 3 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 24 | 8 | 1 | 1 | -1 | x8+ 52x4+ 196 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 3 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 24 | 8 | 1 | 1 | 1 | x8+ 16x7+ 16 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 3 | -1, -2, 2 | x4+ 6x2+ 1
|
| 24 | 8 | 1 | 1 | -1 | x8+ 60x4+ 100 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 3 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 24 | 8 | 1 | 1 | 1 | x8+ 20x4+ 164 | $(C_4\times C_2):C_2$
| $D_4$
|
| 3 | -1, -2, 2 | x4+ 6x2+ 1
|
| 24 | 8 | 1 | 1 | -1 | x8+ 16x4+ 144 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 3 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 24 | 8 | 1 | 1 | 1 | x8+ 32x4+ 144 | $(C_4\times C_2):C_2$
| $C_4\times C_2$
|
| 3 | -1, -2, 2 | x4+ 6x2+ 1
|
| 24 | 8 | 1 | 1 | 1 | x8+ 4x6+ 10x4+ 4x2+ 8x+ 6 | $(C_4\times C_2):C_2$
| $Q_8$
|
| 3 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x7+ 4x6+ 6x4+ 12x2+ 8x+ 10 | $(C_4\times C_2):C_2$
| $Q_8$
|
| 3 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 24 | 8 | 1 | 1 | -1 | x8+ 116x4+ 100 | $D_4\times C_2$
| $D_4$
|
| 3 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
x4+ 6
x4+ 22
|
| 24 | 8 | 1 | 1 | -1 | x8+ 14x4+ 8x3+ 4x2+ 8x+ 14 | $D_4\times C_2$
| $D_4$
|
| 3 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
x4+ 30
x4+ 14
|
| 24 | 8 | 1 | 1 | -1 | x8+ 48x4+ 16 | $D_4\times C_2$
| $C_4\times C_2$
|
| 3 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
x4+ 8x+ 10
x4+ 4x2+ 14
|
| 24 | 8 | 1 | 1 | 1 | x8+ 8x5+ 14x4+ 8x3+ 4x2+ 8x+ 14 | $(C_4\times C_2):C_2$
| $Q_8$
|
| 3 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x2+ 8x+ 6 | T29
| T18
|
| 51/16 | 2* | x4+ 6x2- 1
|
| 24 | 8 | 1 | 1 | 1 | x8+ 12x4+ 8x+ 2 | T29
| T18
|
| 51/16 | 2 | x4+ 2x2- 1
|
| 24 | 8 | 1 | 1 | 1 | x8+ 8x3+ 8x+ 6 | T29
| T18
|
| 51/16 | 2* | x4+ 2x2- 9
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x3+ 8x2+ 8x+ 6 | T29
| T18
|
| 51/16 | 2* | x4+ 2x2- 9
|
| 24 | 8 | 1 | 1 | 1 | x8+ 4x4+ 8x+ 6 | T29
| T18
|
| 51/16 | -2 | x4- 2x2+ 3
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x6+ 16x3+ 8 | T29
| T18
|
| 51/16 | -2 | x4+ 2x2+ 3
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x2+ 8x+ 14 | T29
| T18
|
| 51/16 | 2 | x4+ 6x2- 9
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x2+ 8x+ 10 | T29
| T18
|
| 51/16 | -2* | x4+ 6x2+ 3
|
| 24 | 8 | 1 | 1 | 1 | x8+ 8x+ 2 | T29
| T18
|
| 51/16 | -2 | x4+ 2x2+ 3
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x3+ 8x2+ 8x+ 10 | T29
| T18
|
| 51/16 | -2* | x4- 6x2+ 3
|
| 24 | 8 | 1 | 1 | -1 | x8+ 8x3+ 8x2+ 8x+ 2 | T29
| T18
|
| 51/16 | -2 | x4- 2x2+ 3
|
| 24 | 8 | 1 | 1 | -1 | x8+ 4x4+ 8x2+ 8x+ 2 | T29
| T18
|
| 51/16 | 2 | x4+ 2x2- 1
|
| 24 | 8 | 1 | 1 | 1 | x8+ 8x+ 14 | T29
| T18
|
| 51/16 | 2 | x4+ 6x2- 9
|
| 24 | 8 | 1 | 1 | 1 | x8+ 8x+ 6 | T29
| T18
|
| 51/16 | 2* | x4+ 6x2- 1
|
| 24 | 8 | 1 | 1 | 1 | x8+ 8x+ 10 | T29
| T18
|
| 51/16 | -2* | x4+ 6x2+ 3
|
| 24 | 8 | 1 | 1 | 1 | x8+ 8x4+ 8x+ 10 | T29
| T18
|
| 51/16 | -2* | x4- 6x2+ 3
|
| 24 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x3+ 8x+ 14 | $(C_2^4:C_3):C_2$
| T18
|
| 51/16 | -2* |
|
| 24 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x2+ 8x+ 2 | $(C_2^4:C_3):C_2$
| T18
|
| 51/16 | 2 |
|
| 24 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x+ 6 | $(C_2^4:C_3):C_2$
| T18
|
| 51/16 | -2 |
|
| 24 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x+ 2 | $(C_2^4:C_3):C_2$
| T18
|
| 51/16 | 2 |
|
| 24 | 8 | 1 | 1 | -1 | x8+ 4x6+ 4x4+ 8x+ 6 | $(C_2^4:C_3):C_2$
| T18
|
| 51/16 | 2* |
|
| 24 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x3+ 8x+ 6 | $(C_2^4:C_3):C_2$
| T18
|
| 51/16 | -2 |
|
| 24 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x+ 14 | $(C_2^4:C_3):C_2$
| T18
|
| 51/16 | -2* |
|
| 24 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x+ 10 | $(C_2^4:C_3):C_2$
| T18
|
| 51/16 | 2* |
|
| 24 | 8 | 1 | * | 1 | x8+ 4x6+ 2x4+ 4x2+ 8x+ 2 | $D_8$
| $D_4$
|
| 3 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | 1 | x8+ 20x4+ 52 | $QD_{16}$
| $Q_8$
|
| 3 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | 1 | x8+ 4x6+ 8x5+ 2x4+ 12x2+ 8x+ 2 | $D_8$
| $D_4$
|
| 3 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | 1 | x8+ 4x4+ 84 | $QD_{16}$
| $Q_8$
|
| 3 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 20x6+ 24x4+ 28x2+ 29 | $C_4^2:C_2$
| $D_4$
|
| 3 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 60x4+ 148 | $C_4^2:C_2$
| $Q_8$
|
| 3 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | -1 | x8+ 8x7+ 12x6+ 6x4+ 12x2+ 8x+ 22 | $C_4^2:C_2$
| $D_4$
|
| 3 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 52x4+ 180 | $C_4^2:C_2$
| $Q_8$
|
| 3 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | -1 | x8+ 8x7+ 2x4+ 8x3+ 4x2+ 8x+ 6 | $C_4^2:C_2$
| $D_4$
|
| 3 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 2x4+ 8x3+ 4x2+ 8x+ 6 | $C_4^2:C_2$
| $D_4$
|
| 3 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 4x4+ 20 | $C_4^2:C_2$
| $Q_8$
|
| 3 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | -1 | x8+ 12x4+ 52 | $C_4^2:C_2$
| $Q_8$
|
| 3 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | 1 | x8- 3 | $(C_8\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 8x7+ 14x4+ 4x2+ 8x+ 2 | $(C_8\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | -1 | x8+ 16x7+ 16x4+ 80 | $(C_8\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | 1 | x8+ 80 | $(C_8\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 48x4+ 464 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | -1 | x8+ 16x4+ 464 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | -1 | x8+ 16x4+ 336 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | 1 | x8+ 16x6+ 80 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | 1 | x8+ 48x6+ 80 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | 1 | x8+ 16x7+ 464 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 48x4+ 336 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -1 | x4+ 6x2+ 4x+ 2
|
| 24 | 8 | 1 | * | 1 | x8+ 16x7+ 80 | $C_4^2:C_2$
| $(C_4\times C_2):C_2$
|
| 25/8 | -* | x4+ 2x2+ 4x+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 8x6+ 2x4+ 8x+ 2 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4- 2x2+ 2
|
| 24 | 8 | 1 | * | 1 | x8+ 2x4+ 8x+ 14 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4- 2x2+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 4x6+ 8x5+ 6x4+ 8x+ 2 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4- 2x2+ 2
|
| 24 | 8 | 1 | * | 1 | x8+ 10x4+ 8x+ 10 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 6x2+ 10
|
| 24 | 8 | 1 | * | -1 | x8+ 4x6+ 2x4+ 8x+ 2 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 6x2+ 2
|
| 24 | 8 | 1 | * | -1 | x8+ 4x6+ 2x4+ 8x+ 10 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 6x2+ 10
|
| 24 | 8 | 1 | * | -1 | x8+ 12x6+ 14x4+ 8x+ 2 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 6x2+ 2
|
| 24 | 8 | 1 | * | 1 | x8+ 14x4+ 8x+ 14 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x2- 2
|
| 24 | 8 | 1 | * | 1 | x8+ 10x4+ 8x+ 6 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x2- 2
|
| 24 | 8 | 1 | * | 1 | x8+ 2x4+ 8x+ 2 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4- 2x2+ 2
|
| 24 | 8 | 1 | * | -1 | x8+ 12x6+ 14x4+ 8x+ 14 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x2- 2
|
| 24 | 8 | 1 | * | -1 | x8+ 10x4+ 8x3+ 8x+ 6 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x2+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 2x4+ 8x3+ 8x+ 2 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x2+ 10
|
| 24 | 8 | 1 | * | -1 | x8+ 2x4+ 8x3+ 8x+ 14 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4- 2x2- 2
|
| 24 | 8 | 1 | * | 1 | x8+ 20x6+ 40x2+ 84 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 6x2+ 10
|
| 24 | 8 | 1 | * | -1 | x8+ 8x6+ 6x4+ 8x+ 2 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 6x2+ 10
|
| 24 | 8 | 1 | * | 1 | x8+ 6x4+ 8x+ 6 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4- 2x2+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 8x6+ 10x4+ 8x+ 14 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x2+ 6
|
| 24 | 8 | 1 | * | 1 | x8+ 10x4+ 8x+ 14 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x2+ 6
|
| 24 | 8 | 1 | * | 1 | x8+ 14x4+ 8x+ 6 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x2+ 6
|
| 24 | 8 | 1 | * | 1 | x8+ 14x4+ 8x+ 2 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x2+ 10
|
| 24 | 8 | 1 | * | -1 | x8+ 2x4+ 8x3+ 8x+ 6 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4- 2x2+ 6
|
| 24 | 8 | 1 | * | 1 | x8+ 6x4+ 8x+ 10 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 6x2+ 2
|
| 24 | 8 | 1 | * | 1 | x8+ 20x4+ 16x3+ 40 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4- 2x2+ 2
|
| 24 | 8 | 1 | * | 1 | x8+ 2x4+ 8x+ 6 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4- 2x2- 2
|
| 24 | 8 | 1 | * | -1 | x8+ 12x6+ 8x5+ 10x4+ 8x+ 14 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4+ 2x2- 2
|
| 24 | 8 | 1 | * | 1 | x8+ 2x4+ 8x+ 10 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x2+ 10
|
| 24 | 8 | 1 | * | -1 | x8+ 6x4+ 8x3+ 8x+ 6 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4- 2x2- 2
|
| 24 | 8 | 1 | * | 1 | x8+ 12x4+ 16x3+ 8 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 6x2+ 2
|
| 24 | 8 | 1 | * | -1 | x8+ 4x6+ 2x4+ 8x+ 6 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4- 2x2+ 6
|
| 24 | 8 | 1 | * | -1 | x8+ 4x6+ 14x4+ 8x3+ 8x+ 2 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -1 | x4+ 2x2+ 10
|
| 24 | 8 | 1 | * | 1 | x8+ 6x4+ 8x+ 14 | T35
| T29
|
| [2, 2, 3, 7/2, 7/2, 15/4] | 2 | | |
| 111/32 | -* | x4- 2x2- 2
|
| 24 | 8 | 1 | -1 | i | x8+ 8x5+ 12x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -1 | i | x8+ 4x6+ 12x2+ 8x+ 30 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -1 | i | x8+ 8x6+ 12x2+ 8x+ 18 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -1 | -i | x8+ 4x2+ 8x+ 18 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -1 | -i | x8+ 8x5+ 4x4+ 8x3+ 4x2+ 8x+ 26 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -1 | -i | x8+ 8x7+ 12x6+ 12x4+ 8x3+ 12x2+ 8x+ 6 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -1 | -i | x8+ 12x6+ 4x4+ 12x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -1 | i | x8+ 8x7+ 4x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -1 | -i | x8+ 8x5+ 12x4+ 4x2+ 8x+ 6 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -1 | -i | x8+ 4x2+ 8x+ 10 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -1 | -i | x8+ 12x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -1 | -i | x8+ 12x2+ 8x+ 10 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -1 | i | x8+ 12x4+ 4x2+ 8x+ 30 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -1 | i | x8+ 4x4+ 4x2+ 8x+ 22 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -1 | i | x8+ 12x4+ 4x2+ 8x+ 22 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -1 | i | x8+ 12x6+ 8x5+ 4x4+ 12x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -* | -i | x8+ 8x5+ 4x4+ 12x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -* | -i | x8+ 8x7+ 4x4+ 4x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -* | -i | x8+ 4x6+ 16x3+ 120 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -* | -i | x8+ 8x5+ 4x4+ 4x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -* | -i | x8+ 4x2+ 8x+ 14 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -* | i | x8+ 4x4+ 12x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -* | i | x8+ 8x7+ 8x3+ 4x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -* | -i | x8+ 4x2+ 8x+ 30 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -* | i | x8+ 24x6+ 8x4+ 48 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -* | i | x8+ 8x7+ 12x2+ 8x+ 22 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -* | -i | x8+ 4x2+ 8x+ 6 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -* | i | x8+ 8x7+ 12x2+ 8x+ 30 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -* | -i | x8+ 8x5+ 12x4+ 4x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -* | i | x8+ 8x7+ 12x2+ 8x+ 14 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x+ 2
|
| 24 | 8 | 1 | -* | i | x8+ 4x4+ 12x2+ 8x+ 18 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
| 24 | 8 | 1 | -* | i | x8+ 12x4+ 4x2+ 8x+ 2 | T44
| T38
|
| [2, 8/3, 8/3, 10/3, 10/3, 4] | 2 | | 3 |
| 85/24 | | x4+ 4x2+ 4x+ 2
|
|
|
| 25 | 8 | 1 | 2 | 1 | x8+ 8x7+ 2x4+ 4x2+ 16x+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2, 2 | x4+ 6x2+ 1
|
| 25 | 8 | 1 | 2 | -1 | x8+ 10x4+ 20x2+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2, 2 | x4+ 6x2+ 1
|
| 25 | 8 | 1 | 2 | -1 | x8+ 10x4+ 12x2+ 18 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2, 2 | x4+ 6x2+ 1
|
| 25 | 8 | 1 | 2 | -1 | x8+ 2x4+ 12x2+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2, 2 | x4+ 6x2+ 1
|
| 25 | 8 | 1 | 2 | -1 | x8+ 2x4+ 28x2+ 16x+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2, 2 | x4+ 6x2+ 1
|
| 25 | 8 | 1 | 2 | 1 | x8+ 4x6+ 4x4+ 8 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2, 2 | x4+ 6x2+ 1
|
| 25 | 8 | 1 | 2 | 1 | x8+ 10x4+ 28x2+ 18 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2, 2 | x4+ 6x2+ 1
|
| 25 | 8 | 1 | 2 | 1 | x8+ 2x4+ 4x2+ 18 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2, 2 | x4+ 6x2+ 1
|
| 25 | 8 | 1 | 2 | 1 | x8+ 6x4+ 12x2+ 18 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 6x4+ 20x2+ 2 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 8x5+ 6x4+ 28x2+ 18 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 14x4+ 28x2+ 2 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 6x4+ 4x2+ 18 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 14x4+ 12x2+ 18 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 14x4+ 12x2+ 2 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 6x4+ 4x2+ 2 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 4x2+ 2 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 12x4+ 12x2+ 2 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 4x4+ 12x2+ 18 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 4x4+ 4x2+ 2 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 12x2+ 2 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 4x4+ 12x2+ 2 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 4x2+ 18 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 12x6+ 72 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 4x6+ 72 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 12x4+ 4x2+ 18 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 12x6+ 8 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 28x6+ 72 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 12x2+ 18 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 4x4+ 4x2+ 18 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | 1 | x8+ 12x4+ 8x3+ 12x2+ 30 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2 | -1 | x8+ 12x4+ 4x2+ 2 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 2x4+ 12x2+ 10 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 25 | 8 | 1 | 2* | -1 | x8+ 10x4+ 4x2+ 26 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 25 | 8 | 1 | 2* | 1 | x8+ 12x6+ 14x4+ 4x2+ 26 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 25 | 8 | 1 | 2* | 1 | x8+ 10x4+ 12x2+ 10 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 25 | 8 | 1 | 2* | -1 | x8+ 10x4+ 28x2+ 10 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 25 | 8 | 1 | 2* | -1 | x8+ 2x4+ 28x2+ 10 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 25 | 8 | 1 | 2* | 1 | x8+ 20x6+ 20x4+ 40 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 25 | 8 | 1 | 2* | -1 | x8+ 28x6+ 20x4+ 40 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1, -2*, 2* | x4+ 2x2+ 4x+ 10
|
| 25 | 8 | 1 | 2* | 1 | x8+ 14x4+ 4x2+ 26 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 8x7+ 4x6+ 2x4+ 8x3+ 4x2+ 16x+ 2 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 6x4+ 8x3+ 20x2+ 2 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 4x6+ 2x4+ 8x3+ 4x2+ 18 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 6x4+ 4x2+ 10 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 4x6+ 8x5+ 2x4+ 8x3+ 4x2+ 16x+ 2 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 6x4+ 12x2+ 10 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 14x4+ 12x2+ 10 | T35
| T31
|
| 123/32 | -1 | x4+ 6x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 4x4+ 20x2+ 10 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 12x6+ 104 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 4x4+ 12x2+ 10 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 12x6+ 4x4+ 4x2+ 16x+ 10 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 4x6+ 104 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 4x2+ 26 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 4x4+ 28x2+ 10 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 4x2+ 10 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 4x6+ 40 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 12x6+ 40 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 8x7+ 8x5+ 12x4+ 8x3+ 4x2+ 14 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 12x2+ 26 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 20x2+ 26 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 12x4+ 4x2+ 26 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | -1 | x8+ 12x4+ 12x2+ 10 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | 2* | 1 | x8+ 12x4+ 4x2+ 10 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2 | -i | x8+ 4x6+ 20x4+ 56 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 25 | 8 | 1 | -2 | -i | x8+ 6x4+ 28x2+ 30 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 25 | 8 | 1 | -2 | -i | x8+ 14x4+ 28x2+ 14 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 25 | 8 | 1 | -2 | i | x8+ 14x4+ 4x2+ 30 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 25 | 8 | 1 | -2 | i | x8+ 6x4+ 4x2+ 30 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 25 | 8 | 1 | -2 | i | x8+ 6x4+ 4x2+ 14 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 25 | 8 | 1 | -2 | -i | x8+ 4x6+ 2x4+ 4x2+ 16x+ 14 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 25 | 8 | 1 | -2 | i | x8+ 28x6+ 4x4+ 56 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2*, 2 | x4+ 6x2+ 4x+ 14
|
| 25 | 8 | 1 | -2 | -i | x8+ 10x4+ 4x2+ 30 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2 | -i | x8+ 4x6+ 28x4+ 120 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2 | i | x8+ 28x6+ 28x4+ 56 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2 | i | x8+ 8x7+ 2x4+ 4x2+ 30 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2 | i | x8+ 10x4+ 28x2+ 30 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2 | -i | x8+ 2x4+ 4x2+ 30 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2 | -i | x8+ 8x5+ 2x4+ 8x3+ 28x2+ 16x+ 6 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2 | i | x8+ 2x4+ 8x3+ 4x2+ 6 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2 | -i | x8+ 4x4+ 20x2+ 14 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2 | -i | x8+ 28x6+ 24x4+ 120 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2 | -i | x8+ 4x2+ 14 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2 | i | x8+ 20x6+ 120 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2 | -i | x8+ 4x4+ 20x2+ 16x+ 14 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2 | i | x8+ 28x6+ 120 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2 | i | x8+ 20x2+ 14 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2 | -i | x8+ 12x6+ 56 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2 | i | x8+ 12x4+ 12x2+ 30 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2 | -i | x8+ 8x5+ 4x4+ 28x2+ 22 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2 | -i | x8+ 12x6+ 120 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2 | i | x8+ 4x4+ 12x2+ 14 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2 | i | x8+ 12x4+ 12x2+ 14 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2 | i | x8+ 8x5+ 12x4+ 4x2+ 6 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2 | i | x8+ 28x2+ 14 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2 | -i | x8+ 4x2+ 30 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2* | -i | x8+ 6x4+ 4x2+ 6 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | i | x8+ 4x6+ 2x4+ 8x3+ 12x2+ 6 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | -i | x8+ 8x7+ 4x6+ 10x4+ 28x2+ 22 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | i | x8+ 4x6+ 20x4+ 88 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | i | x8+ 4x6+ 2x4+ 8x3+ 4x2+ 6 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | i | x8+ 8x5+ 14x4+ 4x2+ 6 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | -i | x8+ 4x6+ 2x4+ 4x2+ 6 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | -i | x8+ 6x4+ 4x2+ 22 | T31
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -*, -2, 2* | x4+ 6x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | -i | x8+ 8x5+ 10x4+ 20x2+ 22 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | i | x8+ 10x4+ 4x2+ 6 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | i | x8+ 2x4+ 4x2+ 6 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | -i | x8+ 2x4+ 28x2+ 22 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | i | x8+ 8x5+ 2x4+ 4x2+ 6 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | -i | x8+ 10x4+ 20x2+ 22 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | -i | x8+ 8x5+ 2x4+ 4x2+ 16x+ 6 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | i | x8+ 2x4+ 4x2+ 22 | T35
| T31
|
| 123/32 | -* | x4+ 2x2+ 4x+ 6
|
| 25 | 8 | 1 | -2* | -i | x8+ 4x4+ 4x2+ 22 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2* | -i | x8+ 4x4+ 4x2+ 6 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2* | i | x8+ 4x6+ 88 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2* | -i | x8+ 28x2+ 6 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2* | i | x8+ 4x4+ 28x2+ 22 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2* | i | x8+ 4x4+ 28x2+ 6 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2* | -i | x8+ 20x6+ 88 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2* | -i | x8+ 12x4+ 4x2+ 22 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2* | i | x8+ 12x2+ 6 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2* | i | x8+ 4x2+ 6 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2* | -i | x8+ 20x2+ 6 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2* | i | x8+ 8x5+ 4x4+ 28x2+ 14 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2* | -i | x8+ 20x6+ 24 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
| 25 | 8 | 1 | -2* | i | x8+ 8x5+ 4x4+ 20x2+ 30 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2* | -i | x8+ 12x4+ 12x2+ 22 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x2+ 4x+ 2
|
| 25 | 8 | 1 | -2* | i | x8+ 12x6+ 88 | T44
| T38
|
| [8/3, 8/3, 3, 23/6, 23/6, 17/4] | 2 | | 3 |
| 373/96 | | x4+ 4x+ 2
|
|
|
| 26 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x3+ 8x2+ 2 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2 | x4+ 6x2- 9
x4+ 8x+ 14
x4+ 14
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x7+ 12x6+ 12x4+ 8x3+ 30 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2 | x4+ 2x2- 1
x4+ 4x2+ 18
x4+ 14
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x5+ 8x3+ 2 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2 | x4+ 2x2- 1
x4+ 8x+ 14
x4+ 30
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x7+ 12x6+ 8x5+ 8x4+ 8x3+ 2 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2 | x4+ 6x2- 9
x4+ 12x2+ 2
x4+ 14
|
| 26 | 8 | 1 | 1 | -1 | x8+ 12x6+ 8x5+ 8x3+ 18 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2 | x4+ 2x2- 1
x4+ 12x2+ 18
x4+ 14
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x7+ 4x6+ 8x5+ 12x4+ 8x3+ 8x2+ 6 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2* | x4+ 2x2- 9
x4+ 12x2+ 10
x4+ 6
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 12x4+ 8x3+ 6 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2* | x4+ 2x2- 9
x4+ 8x+ 6
x4+ 22
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x7+ 4x6+ 8x5+ 8x3+ 2 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2 | x4+ 2x2- 1
x4+ 12x2+ 2
x4+ 30
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x7+ 4x6+ 4x4+ 8x3+ 6 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2* | x4+ 6x2- 1
x4+ 8x+ 6
x4+ 6
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x7+ 12x6+ 12x4+ 8x3+ 22 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2* | x4+ 2x2- 9
x4+ 4x2+ 10
x4+ 6
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x7+ 4x6+ 12x4+ 8x3+ 22 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2* | x4+ 2x2- 9
x4+ 8x2+ 8x+ 22
x4+ 22
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x5+ 8x4+ 8x3+ 26 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2* | x4+ 6x2- 1
x4+ 8x2+ 8x+ 22
x4+ 6
|
| 26 | 8 | 1 | 1 | 1 | x8+ 12x6+ 8x3+ 8x2+ 18 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2 | x4+ 6x2- 9
x4+ 12x2+ 18
x4+ 30
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x7+ 4x6+ 8x3+ 8x2+ 10 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2* | x4+ 6x2- 1
x4+ 12x2+ 10
x4+ 22
|
| 26 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x3+ 8x2+ 18 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2 | x4+ 6x2- 9
x4+ 4x2+ 18
x4+ 30
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x7+ 4x6+ 4x4+ 8x3+ 22 | $(C_4\times C_2):C_2$
| $(C_4\times C_2):C_2$
|
| 27/8 | 2* | x4+ 6x2- 1
x4+ 4x2+ 10
x4+ 22
|
| 26 | 8 | 1 | 1 | -1 | x8+ 12x6+ 4x4+ 8x3+ 2 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2 | x4+ 2x2+ 3
x4+ 4x2+ 6
x4+ 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x7+ 4x6+ 4x4+ 8x3+ 18 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2 | x4+ 2x2+ 3
x4+ 4x2+ 6
x4+ 18
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x7+ 4x6+ 12x4+ 8x3+ 10 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2* | x4- 6x2+ 3
x4+ 8x+ 10
x4+ 26
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 4x4+ 8x3+ 10 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2* | x4+ 6x2+ 3
x4+ 8x+ 10
x4+ 10
|
| 26 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x3+ 8x2+ 14 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2* | x4- 6x2+ 3
x4+ 8x+ 10
x4+ 10
|
| 26 | 8 | 1 | 1 | -1 | x8+ 12x6+ 12x4+ 8x3+ 2 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2 | x4- 2x2+ 3
x4+ 12x2+ 6
x4+ 18
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 12x4+ 8x3+ 2 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2 | x4- 2x2+ 3
x4+ 4x2+ 6
x4+ 18
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 12x4+ 8x3+ 26 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2* | x4- 6x2+ 3
x4+ 4x2+ 14
x4+ 10
|
| 26 | 8 | 1 | 1 | -1 | x8+ 12x6+ 8x5+ 8x3+ 14 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2* | x4+ 6x2+ 3
x4+ 4x2+ 14
x4+ 26
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 12x4+ 8x3+ 18 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2 | x4- 2x2+ 3
x4+ 4x2+ 6
x4+ 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x4+ 8x3+ 8x2+ 14 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2* | x4+ 6x2+ 3
x4+ 4x2+ 14
x4+ 10
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 12x4+ 8x3+ 10 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2* | x4- 6x2+ 3
x4+ 4x2+ 14
x4+ 26
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x5+ 8x3+ 30 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2* | x4+ 6x2+ 3
x4+ 8x+ 10
x4+ 26
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x7+ 12x6+ 8x5+ 8x3+ 22 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2 | x4+ 2x2+ 3
x4+ 12x2+ 6
x4+ 18
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x7+ 4x6+ 8x4+ 8x3+ 8x2+ 22 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2 | x4+ 2x2+ 3
x4+ 12x2+ 6
x4+ 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x3+ 8x2+ 6 | T18
| $(C_4\times C_2):C_2$
|
| 27/8 | -2 | x4- 2x2+ 3
x4+ 12x2+ 6
x4+ 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 12x6+ 8x3+ 6 | T29
| T18
|
| 55/16 | -2 | x4+ 2x2+ 3
|
| 26 | 8 | 1 | 1 | -1 | x8+ 12x6+ 8x3+ 10 | T29
| T18
|
| 55/16 | 2* | x4+ 2x2- 9
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x3+ 10 | T29
| T18
|
| 55/16 | 2* | x4+ 2x2- 9
|
| 26 | 8 | 1 | 1 | -1 | x8+ 12x6+ 8x3+ 2 | T29
| T18
|
| 55/16 | 2 | x4+ 2x2- 1
|
| 26 | 8 | 1 | 1 | -1 | x8+ 12x6+ 8x4+ 8x3+ 14 | T29
| T18
|
| 55/16 | -2* | x4- 6x2+ 3
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x3+ 6 | T29
| T18
|
| 55/16 | -2 | x4+ 2x2+ 3
|
| 26 | 8 | 1 | 1 | -1 | x8+ 96x6+ 84x4+ 292 | T29
| T18
|
| 55/16 | -2 | x4- 2x2+ 3
|
| 26 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x5+ 4x4+ 8x3+ 6 | T29
| T18
|
| 55/16 | 2* | x4+ 6x2- 1
|
| 26 | 8 | 1 | 1 | 1 | x8+ 16x5+ 28x4+ 60 | T29
| T18
|
| 55/16 | 2 | x4+ 6x2- 9
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x3+ 2 | T29
| T18
|
| 55/16 | 2 | x4+ 2x2- 1
|
| 26 | 8 | 1 | 1 | -1 | x8+ 12x6+ 8x5+ 8x3+ 8x2+ 2 | T29
| T18
|
| 55/16 | 2 | x4+ 6x2- 9
|
| 26 | 8 | 1 | 1 | -1 | x8+ 12x6+ 8x3+ 14 | T29
| T18
|
| 55/16 | -2* | x4+ 6x2+ 3
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x7+ 12x6+ 8x4+ 8x3+ 10 | T29
| T18
|
| 55/16 | 2* | x4+ 6x2- 1
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x5+ 8x3+ 8x2+ 14 | T29
| T18
|
| 55/16 | -2* | x4- 6x2+ 3
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x5+ 8x3+ 8x2+ 6 | T29
| T18
|
| 55/16 | -2 | x4- 2x2+ 3
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 8x3+ 14 | T29
| T18
|
| 55/16 | -2* | x4+ 6x2+ 3
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x6+ 8x3+ 8x2+ 2 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | -2 |
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x3+ 10 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | -2* |
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x3+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | 2* |
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x3+ 2 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | -2 |
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x3+ 14 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | 2 |
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x6+ 4x4+ 8x3+ 14 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | -2* |
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x6+ 8x3+ 8x2+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | 2* |
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x6+ 8x3+ 2 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | -2 |
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x5+ 8x3+ 8x2+ 14 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | 2 |
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x3+ 8x2+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | 2* |
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x6+ 8x3+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | 2* |
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x4+ 8x3+ 6 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | -2 |
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x6+ 8x3+ 10 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | -2* |
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x3+ 8x2+ 10 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | -2* |
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x6+ 8x3+ 14 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | 2 |
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x3+ 8x2+ 14 | T41
| $(C_2^4:C_3):C_2$
|
| [8/3, 8/3, 3, 23/6, 23/6] | 2 | | 3 |
| 169/48 | 2 |
|
| 26 | 8 | 1 | 1 | 1 | x8+ 6x4+ 8x3+ 26 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4- 2x2+ 2
|
| 26 | 8 | 1 | 1 | 1 | x8+ 14x4+ 8x3+ 26 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 6x2+ 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x5+ 2x4+ 8x3+ 10 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 6x2+ 10
|
| 26 | 8 | 1 | 1 | 1 | x8+ 14x4+ 8x3+ 24x2+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4- 2x2+ 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x5+ 10x4+ 8x3+ 16x2+ 18 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 2x2+ 10
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x5+ 2x4+ 8x3+ 10 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 6x2+ 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 6x4+ 8x3+ 16x+ 26 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4- 2x2+ 2
|
| 26 | 8 | 1 | 1 | 1 | x8+ 14x4+ 8x3+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 6x2+ 10
|
| 26 | 8 | 1 | 1 | -1 | x8+ 6x4+ 8x3+ 16x2+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 2x2+ 10
|
| 26 | 8 | 1 | 1 | 1 | x8+ 6x4+ 8x3+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 2x2+ 10
|
| 26 | 8 | 1 | 1 | 1 | x8+ 14x4+ 8x3+ 18 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 6x2+ 10
|
| 26 | 8 | 1 | 1 | -1 | x8+ 4x6+ 8x5+ 2x4+ 8x3+ 24x2+ 18 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 6x2+ 10
|
| 26 | 8 | 1 | 1 | -1 | x8+ 4x6+ 6x4+ 8x3+ 24x2+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4- 2x2+ 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 14x4+ 8x3+ 16x+ 26 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 6x2+ 2
|
| 26 | 8 | 1 | 1 | 1 | x8+ 6x4+ 8x3+ 18 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 2x2+ 10
|
| 26 | 8 | 1 | 1 | -1 | x8+ 14x4+ 8x3+ 16x+ 10 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -1 | x4+ 6x2+ 2
|
| 26 | 8 | 1 | 1 | 1 | x8+ 24x6+ 144 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4+ 2x2- 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 2x4+ 8x3+ 6 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4- 2x2- 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 2x4+ 8x3+ 16x2+ 16x+ 6 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4- 2x2- 2
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x5+ 14x4+ 8x3+ 24x2+ 22 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4- 2x2+ 6
|
| 26 | 8 | 1 | 1 | -1 | x8+ 32x2+ 272 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4+ 2x2+ 6
|
| 26 | 8 | 1 | 1 | 1 | x8+ 2x4+ 8x3+ 16x+ 6 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4- 2x2- 2
|
| 26 | 8 | 1 | 1 | 1 | x8+ 4x6+ 10x4+ 8x3+ 22 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4- 2x2- 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x6+ 16 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4+ 2x2+ 6
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x6+ 144 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4+ 2x2- 2
|
| 26 | 8 | 1 | 1 | 1 | x8+ 10x4+ 8x3+ 8x2+ 22 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4- 2x2+ 6
|
| 26 | 8 | 1 | 1 | -1 | x8+ 8x5+ 6x4+ 8x3+ 30 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4- 2x2+ 6
|
| 26 | 8 | 1 | 1 | 1 | x8+ 8x6+ 10x4+ 8x3+ 14 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4+ 2x2+ 6
|
| 26 | 8 | 1 | 1 | -1 | x8+ 2x4+ 8x3+ 14 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4- 2x2+ 6
|
| 26 | 8 | 1 | 1 | 1 | x8+ 40x6+ 16 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4+ 2x2+ 6
|
| 26 | 8 | 1 | 1 | -1 | x8+ 4x6+ 2x4+ 8x3+ 16x2+ 6 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4+ 2x2- 2
|
| 26 | 8 | 1 | 1 | -1 | x8+ 40x6+ 144 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -* | x4+ 2x2- 2
|
| 26 | 8 | 1 | * | -1 | x8+ 40x6+ 464 | T35
| T29
|
| 123/32 | -1 | x4- 2x2+ 2
|
| 26 | 8 | 1 | * | 1 | x8+ 14x4+ 8x3+ 22 | T35
| T29
|
| 123/32 | -* | x4+ 2x2- 2
|
| 26 | 8 | 1 | * | 1 | x8+ 8x7+ 4x6+ 2x4+ 8x3+ 8x2+ 16x+ 2 | T35
| T29
|
| 123/32 | -1 | x4+ 6x2+ 10
|
| 26 | 8 | 1 | * | 1 | x8+ 4x6+ 6x4+ 8x3+ 24x2+ 6 | T35
| T29
|
| 123/32 | -* | x4+ 2x2- 2
|
| 26 | 8 | 1 | * | 1 | x8+ 14x4+ 8x3+ 30 | T35
| T29
|
| 123/32 | -* | x4+ 2x2+ 6
|
| 26 | 8 | 1 | * | -1 | x8+ 2x4+ 8x3+ 26 | T35
| T29
|
| 123/32 | -1 | x4+ 6x2+ 2
|
| 26 | 8 | 1 | * | -1 | x8+ 8x6+ 14x4+ 8x3+ 14 | T35
| T29
|
| 123/32 | -* | x4+ 2x2+ 6
|
| 26 | 8 | 1 | * | 1 | x8+ 6x4+ 8x3+ 6 | T35
| T29
|
| 123/32 | -* | x4- 2x2- 2
|
| 26 | 8 | 1 | * | 1 | x8+ 8x6+ 464 | T35
| T29
|
| 123/32 | -1 | x4- 2x2+ 2
|
| 26 | 8 | 1 | * | 1 | x8+ 4x6+ 8x5+ 14x4+ 8x3+ 8x2+ 18 | T35
| T29
|
| 123/32 | -1 | x4+ 6x2+ 2
|
| 26 | 8 | 1 | * | -1 | x8+ 40x6+ 16x4+ 336 | T35
| T29
|
| 123/32 | -* | x4- 2x2+ 6
|
| 26 | 8 | 1 | * | -1 | x8+ 8x6+ 336 | T35
| T29
|
| 123/32 | -1 | x4+ 2x2+ 10
|
| 26 | 8 | 1 | * | 1 | x8+ 14x4+ 8x3+ 14 | T35
| T29
|
| 123/32 | -* | x4+ 2x2+ 6
|
| 26 | 8 | 1 | * | -1 | x8+ 14x4+ 8x3+ 24x2+ 14 | T35
| T29
|
| 123/32 | -* | x4- 2x2- 2
|
| 26 | 8 | 1 | * | -1 | x8+ 6x4+ 8x3+ 16x+ 14 | T35
| T29
|
| 123/32 | -* | x4- 2x2+ 6
|
| 26 | 8 | 1 | * | 1 | x8+ 4x6+ 2x4+ 8x3+ 10 | T35
| T29
|
| 123/32 | -1 | x4+ 6x2+ 10
|
| 26 | 8 | 1 | * | -1 | x8+ 2x4+ 8x3+ 10 | T35
| T29
|
| 123/32 | -1 | x4+ 6x2+ 2
|
| 26 | 8 | 1 | * | -1 | x8+ 2x4+ 8x3+ 2 | T35
| T29
|
| 123/32 | -1 | x4+ 6x2+ 10
|
| 26 | 8 | 1 | * | -1 | x8+ 14x4+ 8x3+ 16x+ 30 | T35
| T29
|
| 123/32 | -* | x4+ 2x2+ 6
|
| 26 | 8 | 1 | * | -1 | x8+ 4x6+ 8x5+ 2x4+ 8x3+ 6 | T35
| T29
|
| 123/32 | -* | x4+ 2x2- 2
|
| 26 | 8 | 1 | * | 1 | x8+ 24x6+ 336 | T35
| T29
|
| 123/32 | -1 | x4+ 2x2+ 10
|
| 26 | 8 | 1 | * | 1 | x8+ 6x4+ 8x3+ 14 | T35
| T29
|
| 123/32 | -* | x4- 2x2+ 6
|
| 26 | 8 | 1 | * | 1 | x8+ 8x6+ 6x4+ 8x3+ 16x2+ 14 | T35
| T29
|
| 123/32 | -* | x4- 2x2+ 6
|
| 26 | 8 | 1 | * | -1 | x8+ 8x6+ 80 | T35
| T29
|
| 123/32 | -1 | x4+ 2x2+ 10
|
| 26 | 8 | 1 | * | 1 | x8+ 4x6+ 2x4+ 8x3+ 16x+ 2 | T35
| T29
|
| 123/32 | -1 | x4+ 6x2+ 2
|
| 26 | 8 | 1 | * | -1 | x8+ 8x7+ 8x5+ 14x4+ 8x3+ 16x+ 2 | T35
| T29
|
| 123/32 | -1 | x4+ 6x2+ 10
|
| 26 | 8 | 1 | * | 1 | x8+ 8x5+ 2x4+ 8x3+ 6 | T35
| T29
|
| 123/32 | -* | x4- 2x2- 2
|
| 26 | 8 | 1 | * | 1 | x8+ 24x6+ 80 | T35
| T29
|
| 123/32 | -1 | x4+ 2x2+ 10
|
| 26 | 8 | 1 | * | -1 | x8+ 32x2+ 80 | T35
| T29
|
| 123/32 | -1 | x4- 2x2+ 2
|
| 26 | 8 | 1 | * | -1 | x8+ 4x6+ 8x5+ 2x4+ 8x3+ 16x+ 6 | T35
| T29
|
| 123/32 | -* | x4+ 2x2- 2
|
| 26 | 8 | 1 | * | -1 | x8+ 8x7+ 8x5+ 2x4+ 8x3+ 6 | T35
| T29
|
| 123/32 | -* | x4- 2x2- 2
|
| 26 | 8 | 1 | * | 1 | x8+ 8x6+ 208 | T35
| T29
|
| 123/32 | -1 | x4- 2x2+ 2
|
|
|
| 27 | 8 | 1 | 2 | 1 | x8+ 4x6+ 6x4+ 2 | $D_8$
| $D_8$
|
| 29/8 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 4x6+ 6x4+ 18 | $D_8$
| $D_8$
|
| 29/8 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 4x6+ 2x4+ 24x2+ 18 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 4x6+ 14x4+ 16x3+ 18 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 8x5+ 6x4+ 18 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 4x6+ 6x4+ 16x+ 18 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 4x6+ 14x4+ 2 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 4x6+ 6x4+ 16x+ 2 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 8x5+ 2x4+ 10 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2 | -1 | x8+ 36x4+ 16x2+ 8 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2 | -1 | x8+ 4x6+ 10x4+ 2 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2 | 1 | x8+ 4x6+ 2x4+ 2 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2 | -1 | x8+ 4x6+ 10x4+ 18 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2 | 1 | x8+ 4x6+ 18x4+ 2 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2 | -1 | x8+ 8x7+ 4x6+ 2x4+ 16x3+ 8x2+ 10 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2 | 1 | x8+ 8x5+ 2x4+ 26 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2 | 1 | x8+ 18x4+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 26x4+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 10x4+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 22x4+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 2x4+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 26x4+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 14x4+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 30x4+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 10x4+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 6x4+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 2x4+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 6x4+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | -1 | x8+ 22x4+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 36x4+ 72 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 18x4+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 14x4+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2 | 1 | x8+ 8x7+ 10x4+ 10 | T35
| T26
|
| 127/32 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2 | -1 | x8+ 12x6+ 8x5+ 2x4+ 24x2+ 10 | T35
| T26
|
| 127/32 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2 | -1 | x8+ 8x7+ 14x4+ 10 | T35
| T26
|
| 127/32 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2 | -1 | x8+ 8x7+ 4x6+ 8x5+ 2x4+ 2 | T35
| T26
|
| 127/32 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2 | 1 | x8+ 8x6+ 12x4+ 8 | T35
| T26
|
| 127/32 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2 | 1 | x8+ 8x7+ 2x4+ 16x+ 10 | T35
| T26
|
| 127/32 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2 | 1 | x8+ 14x4+ 8x2+ 2 | T35
| T26
|
| 127/32 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2 | -1 | x8+ 10x4+ 8x2+ 2 | T35
| T26
|
| 127/32 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 8x5+ 2x4+ 8x2+ 2 | $D_8$
| $D_8$
|
| 29/8 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 8x5+ 22x4+ 16x2+ 26 | $D_8$
| $D_8$
|
| 29/8 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 8x7+ 52x4+ 40 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 4x6+ 6x4+ 10 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 4x6+ 6x4+ 16x+ 26 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 4x6+ 14x4+ 26 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 4x6+ 22x4+ 16x3+ 26 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 4x6+ 14x4+ 10 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 4x6+ 10x4+ 10 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2* | -1 | x8+ 4x6+ 2x4+ 10 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2* | 1 | x8+ 4x6+ 18x4+ 16x+ 26 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2* | 1 | x8+ 4x6+ 26x4+ 10 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2* | 1 | x8+ 8x5+ 10x4+ 18 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2* | -1 | x8+ 8x5+ 18x4+ 2 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2* | -1 | x8+ 4x6+ 2x4+ 26 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2* | -1 | x8+ 8x5+ 2x4+ 2 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2* | -1 | x8+ 14x4+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 12x4+ 104 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 26x4+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 6x4+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 14x4+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 2x4+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 10x4+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 18x4+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 10x4+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 22x4+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 26x4+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 22x4+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 18x4+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 6x4+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 6x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 30x4+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | -1 | x8+ 30x4+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 63/16 | -1 | x4+ 2x2+ 10
|
| 27 | 8 | 1 | 2* | 1 | x8+ 8x7+ 26x4+ 16x+ 2 | T35
| T26
|
| 127/32 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2* | 1 | x8+ 8x6+ 20x4+ 104 | T35
| T26
|
| 127/32 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2* | -1 | x8+ 8x7+ 10x4+ 2 | T35
| T26
|
| 127/32 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2* | 1 | x8+ 10x4+ 8x2+ 10 | T35
| T26
|
| 127/32 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2* | -1 | x8+ 8x7+ 8x6+ 2x4+ 2 | T35
| T26
|
| 127/32 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2* | 1 | x8+ 6x4+ 8x2+ 10 | T35
| T26
|
| 127/32 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | 2* | -1 | x8+ 2x4+ 8x2+ 10 | T35
| T26
|
| 127/32 | -1 | x4+ 6x2+ 2
|
| 27 | 8 | 1 | 2* | -1 | x8+ 8x7+ 14x4+ 16x+ 2 | T35
| T26
|
| 127/32 | -1 | x4- 2x2+ 2
|
| 27 | 8 | 1 | -2 | -i | x8+ 12x6+ 2x4+ 30 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2 | -i | x8+ 60x4+ 16x2+ 56 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2 | -i | x8+ 8x5+ 10x4+ 14 | $D_8$
| $D_8$
|
| 29/8 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2 | -i | x8+ 8x5+ 10x4+ 30 | $D_8$
| $D_8$
|
| 29/8 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2 | i | x8+ 8x6+ 8x5+ 2x4+ 16x3+ 14 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2 | i | x8+ 12x6+ 18x4+ 16x2+ 30 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2 | i | x8+ 12x6+ 10x4+ 14 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2 | i | x8+ 12x6+ 10x4+ 30 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2 | -i | x8+ 12x6+ 14x4+ 30 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2 | -i | x8+ 4x6+ 22x4+ 16x+ 30 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2 | -i | x8+ 52x4+ 48x2+ 56 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2 | -i | x8+ 4x6+ 30x4+ 14 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2 | i | x8+ 4x6+ 6x4+ 14 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2 | i | x8+ 8x5+ 6x4+ 6 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2 | i | x8+ 12x6+ 14x4+ 16x+ 14 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2 | i | x8+ 12x6+ 10x4+ 24x2+ 16x+ 14 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2 | i | x8+ 10x4+ 30 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2 | i | x8+ 14x4+ 30 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2 | i | x8+ 10x4+ 14 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2 | -i | x8+ 2x4+ 30 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2 | -i | x8+ 6x4+ 30 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2 | i | x8+ 14x4+ 14 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2 | -i | x8+ 2x4+ 14 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2 | -i | x8+ 6x4+ 14 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2 | i | x8+ 24x6+ 52x4+ 56 | T35
| T26
|
| 127/32 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2 | -i | x8+ 8x7+ 2x4+ 16x+ 22 | T35
| T26
|
| 127/32 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2 | -i | x8+ 12x6+ 8x5+ 2x4+ 8x2+ 14 | T35
| T26
|
| 127/32 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2 | -i | x8+ 2x4+ 8x2+ 14 | T35
| T26
|
| 127/32 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2 | i | x8+ 14x4+ 8x2+ 30 | T35
| T26
|
| 127/32 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2 | i | x8+ 8x6+ 52x4+ 56 | T35
| T26
|
| 127/32 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2 | i | x8+ 8x7+ 2x4+ 6 | T35
| T26
|
| 127/32 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2 | -i | x8+ 6x4+ 24x2+ 30 | T35
| T26
|
| 127/32 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2* | i | x8+ 8x5+ 10x4+ 22 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2* | i | x8+ 8x5+ 26x4+ 16x+ 6 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2* | i | x8+ 4x6+ 2x4+ 22 | $D_8$
| $D_8$
|
| 29/8 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2* | i | x8+ 4x6+ 2x4+ 6 | $D_8$
| $D_8$
|
| 29/8 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2* | -i | x8+ 8x7+ 8x5+ 14x4+ 16x3+ 22 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2* | -i | x8+ 8x5+ 2x4+ 22 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2* | -i | x8+ 8x5+ 2x4+ 6 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2* | -i | x8+ 12x6+ 10x4+ 22 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2* | -i | x8+ 8x5+ 6x4+ 30 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2* | i | x8+ 12x6+ 14x4+ 6 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2* | -i | x8+ 8x7+ 8x5+ 22x4+ 24x2+ 6 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2* | i | x8+ 8x7+ 8x5+ 18x4+ 16x+ 14 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2* | -i | x8+ 8x6+ 8x5+ 14x4+ 16x+ 30 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2* | i | x8+ 8x6+ 8x5+ 22x4+ 30 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2* | -i | x8+ 8x7+ 60x4+ 56 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2* | i | x8+ 4x6+ 14x4+ 6 | T35
| T26
|
| [2, 2, 3, 7/2, 7/2, 9/2] | 2 | | |
| 123/32 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2* | -i | x8+ 14x4+ 22 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2* | -i | x8+ 10x4+ 22 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2* | i | x8+ 2x4+ 22 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2* | i | x8+ 6x4+ 22 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2* | i | x8+ 6x4+ 6 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2* | i | x8+ 2x4+ 6 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4+ 2x2+ 6
|
| 27 | 8 | 1 | -2* | -i | x8+ 10x4+ 6 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2* | -i | x8+ 14x4+ 6 | T26
| $C_4^2:C_2$
|
| 63/16 | -* | x4- 2x2+ 6
|
| 27 | 8 | 1 | -2* | i | x8+ 8x7+ 12x6+ 8x5+ 22x4+ 6 | T35
| T26
|
| 127/32 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2* | i | x8+ 24x6+ 60x4+ 24 | T35
| T26
|
| 127/32 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2* | -i | x8+ 14x4+ 8x2+ 22 | T35
| T26
|
| 127/32 | -* | x4+ 2x2- 2
|
| 27 | 8 | 1 | -2* | i | x8+ 22x4+ 8x2+ 6 | T35
| T26
|
| 127/32 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2* | i | x8+ 2x4+ 8x2+ 6 | T35
| T26
|
| 127/32 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2* | -i | x8+ 8x6+ 2x4+ 16x3+ 8x2+ 6 | T35
| T26
|
| 127/32 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2* | -i | x8+ 24x6+ 44x4+ 24 | T35
| T26
|
| 127/32 | -* | x4- 2x2- 2
|
| 27 | 8 | 1 | -2* | -i | x8+ 8x7+ 6x4+ 30 | T35
| T26
|
| 127/32 | -* | x4+ 2x2- 2
|
|
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 4x4+ 6 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 2
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x6+ 8x5+ 4x4+ 22 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 2
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x6+ 8x5+ 22 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 8x2+ 8x+ 22
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 16x2+ 14 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 8x+ 14
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x6+ 8x5+ 8x4+ 16x2+ 6 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 8x+ 6
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 16x5+ 56 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 12x2+ 18
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 8x5+ 6 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 12x2+ 10
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x6+ 8x5+ 8x2+ 26 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 10
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 8x2+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 18
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 8x2+ 26 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 10
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 12x4+ 6 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 2
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 8x2+ 16x+ 2 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 18
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 16x2+ 22 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 4x2+ 10
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 14 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 8x+ 14
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 4x4+ 14 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 10
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 12x4+ 14 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 10
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 6 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 8x+ 6
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 8x5+ 8x4+ 30 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 4x2+ 18
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 8x4+ 6 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 12x2+ 10
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 8x5+ 30 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 12x2+ 2
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x6+ 8x5+ 4x4+ 14 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 26
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 4x4+ 30 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 26
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 12x4+ 30 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 26
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x7+ 24x6+ 104 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 26
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 8x4+ 30 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 12x2+ 2
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 16x5+ 24 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 8x2+ 8x+ 22
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 30 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 4x2+ 18
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 12x4+ 22 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 18
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x6+ 8x5+ 4x4+ 6 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 18
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 8x2+ 18 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 2
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x6+ 8x5+ 14 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 12x2+ 18
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 22 | $((C_4\times C_2):C_2):C_2$
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 4x2+ 10
|
| 28 | 8 | 1 | 1 | 1 | x8+ 16x6+ 44x4+ 196 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 6
|
| 28 | 8 | 1 | 1 | 1 | x8+ 60x4+ 96x2+ 100 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 14
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x7+ 8x6+ 120 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 30
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 8x5+ 8x4+ 18 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 12x2+ 6
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 8x5+ 18 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 4x2+ 6
|
| 28 | 8 | 1 | 1 | 1 | x8+ 12x6+ 54x4+ 108x2+ 41 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 6
|
| 28 | 8 | 1 | 1 | 1 | x8+ 108x6+ 6x4+ 44x2+ 25 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 14
|
| 28 | 8 | 1 | 1 | 1 | x8+ 108x6+ 6x4+ 44x2+ 121 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 22
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 12x4+ 26 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 6
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 12x4+ 2 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 14
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 26 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 8x+ 10
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 4x4+ 10 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 6
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x6+ 8x5+ 24x2+ 14 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 30
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 8x2+ 22 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 22
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x6+ 8x5+ 26 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 4x2+ 14
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 8x4+ 18 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 4x2+ 6
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x6+ 8x5+ 16x2+ 26 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 4x2+ 14
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 4x4+ 26 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 22
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 10 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 8x+ 10
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x6+ 8x5+ 10 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 4x2+ 14
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 18 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 12x2+ 6
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 8x5+ 26 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 4x2+ 14
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 16x2+ 10 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 8x+ 10
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 8x6+ 8x5+ 16x2+ 2 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 12x2+ 6
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x6+ 8x5+ 2 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 4x2+ 6
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 8x5+ 8x4+ 10 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2* | x4+ 8x+ 10
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 24x2+ 16x+ 30 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 30
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x7+ 8x5+ 4x4+ 26 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2* | x4+ 22
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 4x4+ 18 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 14
|
| 28 | 8 | 1 | 1 | 1 | x8+ 8x5+ 2 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 12x2+ 6
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x5+ 4x4+ 2 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | 2 | x4+ 30
|
| 28 | 8 | 1 | 1 | -1 | x8+ 8x7+ 8x5+ 2 | T29
| $((C_4\times C_2):C_2):C_2$
|
| 61/16 | -2 | x4+ 4x2+ 6
|
| 28 | 8 | 1 | -1 | -i | x8+ 12x4+ 60 | $D_8$
| $D_8$
|
| 29/8 | 2* | x4+ 2x2- 9
|
| 28 | 8 | 1 | -1 | -i | x8+ 4x4+ 124 | $D_8$
| $D_8$
|
| 29/8 | 2 | x4+ 2x2- 1
|
| 28 | 8 | 1 | -1 | -i | x8+ 8x4+ 496 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | 2 | x4+ 2x2- 1
|
| 28 | 8 | 1 | -1 | -i | x8+ 8x4+ 112 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | 2* | x4+ 2x2- 9
|
| 28 | 8 | 1 | -1 | -i | x8+ 8x4+ 368 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | 2* | x4+ 2x2- 9
|
| 28 | 8 | 1 | -1 | -i | x8+ 8x4+ 240 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | 2 | x4+ 2x2- 1
|
| 28 | 8 | 1 | -1 | -i | x8+ 10x4+ 8x2+ 7 | $D_8$
| $D_8$
|
| 29/8 | 2* | x4+ 2x2- 9
|
| 28 | 8 | 1 | -1 | -i | x8+ 4x4+ 60 | $D_8$
| $D_8$
|
| 29/8 | 2 | x4+ 2x2- 1
|
| 28 | 8 | 1 | -1 | i | x8+ 40x4+ 240 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | 2* | x4+ 6x2- 1
|
| 28 | 8 | 1 | -1 | i | x8+ 12x4+ 28 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | 2 | x4+ 6x2- 9
|
| 28 | 8 | 1 | -1 | i | x8+ 4x4+ 28 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | 2* | x4+ 6x2- 1
|
| 28 | 8 | 1 | -1 | i | x8+ 40x4+ 368 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | 2 | x4+ 6x2- 9
|
| 28 | 8 | 1 | -1 | i | x8+ 4x4+ 92 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | 2* | x4+ 6x2- 1
|
| 28 | 8 | 1 | -1 | i | x8+ 12x4+ 92 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | 2 | x4+ 6x2- 9
|
| 28 | 8 | 1 | -1 | i | x8+ 24x4+ 496 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | 2* | x4+ 6x2- 1
|
| 28 | 8 | 1 | -1 | i | x8+ 24x4+ 368 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | 2 | x4+ 6x2- 9
|
| 28 | 8 | 1 | -1 | i | x8+ 6x4+ 24x2+ 15 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2 | x4+ 6x2- 9
|
| 28 | 8 | 1 | -1 | -i | x8+ 24x6+ 30x4+ 8x2+ 7 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2* | x4+ 6x2- 1
|
| 28 | 8 | 1 | -1 | -i | x8+ 24x6+ 30x4+ 8x2+ 15 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2 | x4+ 6x2- 9
|
| 28 | 8 | 1 | -1 | -i | x8+ 8x7+ 4x6+ 8x5+ 20x4+ 8x2+ 14 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2 | x4+ 2x2- 1
|
| 28 | 8 | 1 | -1 | -i | x8+ 24x6+ 2x4+ 31 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2* | x4+ 2x2- 9
|
| 28 | 8 | 1 | -1 | -i | x8+ 8x7+ 12x6+ 8x5+ 8x2+ 10 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2* | x4+ 6x2- 1
|
| 28 | 8 | 1 | -1 | -i | x8+ 8x7+ 4x6+ 8x5+ 10 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2* | x4+ 2x2- 9
|
| 28 | 8 | 1 | -1 | i | x8+ 4x6+ 8x5+ 2 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2 | x4+ 2x2- 1
|
| 28 | 8 | 1 | -1 | i | x8+ 4x6+ 8x5+ 24x2+ 10 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2* | x4+ 6x2- 1
|
| 28 | 8 | 1 | -1 | i | x8+ 4x6+ 8x5+ 10 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2* | x4+ 2x2- 9
|
| 28 | 8 | 1 | -1 | -i | x8+ 16x6+ 8x4+ 368 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2 | x4+ 2x2- 1
|
| 28 | 8 | 1 | -1 | i | x8+ 8x7+ 48x2+ 40 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2* | x4+ 2x2- 9
|
| 28 | 8 | 1 | -1 | i | x8+ 4x6+ 8x5+ 8x2+ 10 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2* | x4+ 6x2- 1
|
| 28 | 8 | 1 | -1 | i | x8+ 12x6+ 8x5+ 16x3+ 24x2+ 16x+ 2 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2 | x4+ 6x2- 9
|
| 28 | 8 | 1 | -1 | -i | x8+ 24x6+ 14x4+ 8x2+ 15 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2 | x4+ 6x2- 9
|
| 28 | 8 | 1 | -1 | i | x8+ 4x6+ 8x5+ 16x2+ 2 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | 2 | x4+ 2x2- 1
|
| 28 | 8 | 1 | -* | -i | x8+ 8x7+ 4x6+ 8x5+ 14 | $D_8$
| $D_8$
|
| 29/8 | -2* | x4+ 6x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 16x7+ 12x4+ 44 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -2 | x4- 2x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 24x6+ 2x4+ 11 | $D_8$
| $D_8$
|
| 29/8 | -2 | x4+ 2x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 4x6+ 8x5+ 20x4+ 16x3+ 24x2+ 2 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -2 | x4- 2x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 22x4+ 8x2+ 11 | $D_8$
| $D_8$
|
| 29/8 | -2* | x4+ 6x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 4x6+ 8x5+ 24x4+ 14 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -2* | x4- 6x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 16x7+ 60x4+ 44 | $QD_{16}$
| $QD_{16}$
|
| 29/8 | -2* | x4- 6x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 24x6+ 18x4+ 11 | $D_8$
| $D_8$
|
| 29/8 | -2 | x4+ 2x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 4x6+ 8x5+ 8x2+ 6 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -2 | x4- 2x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 8x6+ 26x4+ 11 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -2* | x4- 6x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 4x6+ 8x5+ 6 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -2 | x4+ 2x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 8x6+ 10x4+ 11 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -2* | x4- 6x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 8x6+ 14x4+ 8x2+ 27 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -2* | x4+ 6x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 8x7+ 48x2+ 88 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -2 | x4+ 2x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 12x6+ 8x5+ 20x4+ 2 | $(C_8\times C_2):C_2$
| $D_8$
|
| 29/8 | -2 | x4- 2x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 4x6+ 8x5+ 14 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 29/8 | -2* | x4+ 6x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 20x4+ 44 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2 | x4+ 2x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 12x4+ 12 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2* | x4+ 6x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 4x4+ 12 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2 | x4- 2x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 56x4+ 176 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2* | x4- 6x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 8x4+ 48 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2 | x4+ 2x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 12x4+ 44 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2 | x4- 2x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 4x4+ 44 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2* | x4+ 6x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 20x4+ 12 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2* | x4- 6x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 28x4+ 12 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2 | x4+ 2x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 72x4+ 176 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2* | x4+ 6x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 56x4+ 48 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2 | x4- 2x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 24x4+ 176 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2 | x4+ 2x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 28x4+ 44 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2* | x4- 6x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 40x4+ 176 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2 | x4- 2x2+ 3
|
| 28 | 8 | 1 | -* | -i | x8+ 8x4+ 176 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2* | x4+ 6x2+ 3
|
| 28 | 8 | 1 | -* | i | x8+ 104x4+ 48 | T26
| $(C_8\times C_2):C_2$
|
| 59/16 | -2* | x4- 6x2+ 3
|
|
|
| 29 | 8 | 1 | 2 | -1 | x8+ 28x6+ 2 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | 2 | -1 | x8+ 20x6+ 18 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | 2 | 1 | x8+ 12x6+ 2 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | 2 | -1 | x8+ 28x6+ 16x5+ 8x2+ 2 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | 2 | -1 | x8+ 28x6+ 18 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | 2 | 1 | x8+ 20x6+ 8x4+ 2 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | 2 | 1 | x8+ 12x6+ 18 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | 2 | 1 | x8+ 28x6+ 8x4+ 18 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | 2 | 1 | x8+ 4x6+ 18 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | 2 | -1 | x8+ 12x6+ 8x2+ 18 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | 2 | -1 | x8+ 20x6+ 2 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | 2 | 1 | x8+ 20x6+ 8x2+ 16x+ 2 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | 2 | -1 | x8+ 4x6+ 8x2+ 18 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | 2 | 1 | x8+ 28x6+ 8x2+ 2 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | 2 | -1 | x8+ 12x6+ 8x4+ 2 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | 2 | 1 | x8+ 4x6+ 2 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | 2 | 1 | x8+ 20x6+ 28x4+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | 2 | -1 | x8+ 12x6+ 12x4+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | 2 | -1 | x8+ 4x6+ 4x4+ 16x+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | 2 | -1 | x8+ 28x6+ 20x4+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | 2 | -1 | x8+ 20x6+ 20x4+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | 2 | 1 | x8+ 8x7+ 4x6+ 22 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | 2 | 1 | x8+ 12x6+ 4x4+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | 2 | -1 | x8+ 8x7+ 28x6+ 22 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | 2 | 1 | x8+ 12x6+ 20x4+ 16x3+ 16x+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | 2 | 1 | x8+ 8x7+ 4x6+ 16x+ 22 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | 2 | -1 | x8+ 8x7+ 28x6+ 6 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | 2 | 1 | x8+ 4x6+ 4x4+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | 2 | -1 | x8+ 12x6+ 12x4+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | 2 | -1 | x8+ 8x7+ 20x6+ 16x5+ 8x2+ 6 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | 2 | 1 | x8+ 28x6+ 28x4+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | 2 | 1 | x8+ 20x6+ 4x4+ 16x+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | 2* | 1 | x8+ 20x6+ 10 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | 2* | 1 | x8+ 20x6+ 26 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | 2* | -1 | x8+ 12x6+ 10 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | 2* | -1 | x8+ 8x7+ 4x6+ 16x5+ 28x4+ 6 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | 2* | -1 | x8+ 4x6+ 26 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | 2* | -1 | x8+ 12x6+ 26 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | 2* | 1 | x8+ 28x6+ 24x4+ 16x2+ 10 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | 2* | 1 | x8+ 28x6+ 10 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | 2* | -1 | x8+ 8x6+ 80x2+ 104 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | 2* | 1 | x8+ 4x6+ 8x2+ 26 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | 2* | 1 | x8+ 12x6+ 8x2+ 26 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | 2* | 1 | x8+ 28x6+ 26 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | 2* | 1 | x8+ 12x6+ 8x4+ 10 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | 2* | -1 | x8+ 12x6+ 8x4+ 16x2+ 10 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | 2* | -1 | x8+ 4x6+ 10 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | 2* | -1 | x8+ 20x6+ 24x4+ 26 | T28
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | 2* | 1 | x8+ 8x7+ 4x6+ 16x3+ 30 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | 2* | -1 | x8+ 8x7+ 4x6+ 24x4+ 30 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | 2* | -1 | x8+ 8x7+ 4x6+ 16x5+ 16x3+ 8x2+ 14 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | 2* | 1 | x8+ 8x7+ 4x6+ 16x3+ 14 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | 2* | -1 | x8+ 8x7+ 12x6+ 14 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | 2* | -1 | x8+ 4x6+ 4x4+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | 2* | 1 | x8+ 4x6+ 20x4+ 16x2+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | 2* | 1 | x8+ 4x6+ 12x4+ 26 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | 2* | 1 | x8+ 4x6+ 12x4+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | 2* | -1 | x8+ 8x7+ 28x6+ 24x4+ 16x3+ 8x2+ 14 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | 2* | -1 | x8+ 8x7+ 20x6+ 16x2+ 14 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | 2* | 1 | x8+ 20x6+ 20x4+ 8x2+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | 2* | -1 | x8+ 56x4+ 16x2+ 104 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | 2* | 1 | x8+ 28x6+ 20x4+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | 2* | 1 | x8+ 28x6+ 4x4+ 26 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | 2* | -1 | x8+ 4x6+ 4x4+ 26 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | -2 | -i | x8+ 4x6+ 4x4+ 14 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | -2 | i | x8+ 20x6+ 4x4+ 14 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | -2 | i | x8+ 12x6+ 20x4+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | -2 | i | x8+ 4x6+ 12x4+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | -2 | -i | x8+ 8x4+ 80x2+ 120 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | -2 | i | x8+ 8x7+ 4x6+ 8x2+ 2 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | -2 | -i | x8+ 20x6+ 28x4+ 14 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | -2 | i | x8+ 8x7+ 12x6+ 16x4+ 16x2+ 18 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | -2 | -i | x8+ 8x7+ 12x6+ 18 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | -2 | -i | x8+ 4x6+ 12x4+ 16x3+ 16x+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | -2 | i | x8+ 12x6+ 4x4+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | -2 | i | x8+ 4x6+ 12x4+ 14 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | -2 | -i | x8+ 4x6+ 28x4+ 16x+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | -2 | i | x8+ 4x6+ 12x4+ 16x3+ 16x2+ 16x+ 14 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 6x2- 9
|
| 29 | 8 | 1 | -2 | -i | x8+ 4x6+ 4x4+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | -2 | -i | x8+ 8x7+ 20x6+ 18 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 2x2- 1
|
| 29 | 8 | 1 | -2 | -i | x8+ 16x2+ 56 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | -2 | i | x8+ 4x6+ 16x5+ 16x4+ 8x2+ 16x+ 14 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | -2 | i | x8+ 32x5+ 88x4+ 48 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | -2 | -i | x8+ 12x6+ 30 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | -2 | i | x8+ 28x6+ 30 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | -2 | -i | x8+ 20x6+ 30 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | -2 | i | x8+ 12x6+ 8x4+ 14 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | -2 | i | x8+ 4x6+ 30 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | -2 | -i | x8+ 12x6+ 14 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | -2 | i | x8+ 28x6+ 14 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | -2 | -i | x8+ 4x6+ 24x4+ 14 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | -2 | i | x8+ 4x6+ 14 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 6x2+ 3
|
| 29 | 8 | 1 | -2 | -i | x8+ 4x6+ 8x2+ 16x+ 14 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | -2 | i | x8+ 8x7+ 4x6+ 20x4+ 26 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | -2 | -i | x8+ 20x6+ 16x5+ 8x2+ 14 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | -2 | -i | x8+ 4x6+ 8x2+ 14 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4- 6x2+ 3
|
| 29 | 8 | 1 | -2* | i | x8+ 8x7+ 20x6+ 8x2+ 10 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | -2* | i | x8+ 12x6+ 22 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | -2* | -i | x8+ 4x6+ 22 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | -2* | i | x8+ 20x6+ 22 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | -2* | i | x8+ 4x6+ 8x2+ 6 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | -2* | -i | x8+ 28x6+ 28x4+ 16x+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | -2* | -i | x8+ 8x7+ 4x6+ 8x2+ 10 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | -2* | i | x8+ 28x6+ 8x2+ 22 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | -2* | i | x8+ 8x7+ 4x6+ 4x4+ 16x+ 2 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | -2* | -i | x8+ 4x6+ 28x4+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | -2* | i | x8+ 12x6+ 12x4+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | -2* | i | x8+ 4x6+ 4x4+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | -2* | -i | x8+ 4x6+ 6 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | -2* | -i | x8+ 12x6+ 24x4+ 22 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | -2* | -i | x8+ 32x5+ 88x4+ 432 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | -2* | -i | x8+ 20x6+ 8x4+ 6 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | -2* | -i | x8+ 4x6+ 4x4+ 16x2+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | -2* | -i | x8+ 8x7+ 4x6+ 10 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | -2* | i | x8+ 28x6+ 16x5+ 12x4+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | -2* | i | x8+ 20x6+ 6 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | -2* | i | x8+ 12x6+ 12x4+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | -2* | -i | x8+ 8x7+ 28x6+ 16x5+ 20x4+ 24x2+ 18 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | -2* | -i | x8+ 20x6+ 4x4+ 8x2+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | -2* | i | x8+ 4x6+ 4x4+ 16x2+ 16x+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | -2* | i | x8+ 28x6+ 20x4+ 8x2+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | -2* | i | x8+ 4x6+ 8x2+ 16x+ 22 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4- 2x2+ 3
|
| 29 | 8 | 1 | -2* | i | x8+ 4x6+ 16x5+ 4x4+ 16x+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | -2* | i | x8+ 12x6+ 6 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | -2* | -i | x8+ 28x6+ 6 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
| 29 | 8 | 1 | -2* | -i | x8+ 4x6+ 16x5+ 12x4+ 16x2+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6x2- 1
|
| 29 | 8 | 1 | -2* | -i | x8+ 12x6+ 4x4+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 2x2- 9
|
| 29 | 8 | 1 | -2* | -i | x8+ 28x6+ 22 | T35
| T28
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2x2+ 3
|
|
|
| 30 | 8 | 1 | -1 | -i | x8+ 28x6+ 10x4+ 20x2+ 23 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 4x2+ 18
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 16x3+ 16x+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 14
|
| 30 | 8 | 1 | -1 | -i | x8+ 12x6+ 18x4+ 20x2+ 23 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 12x2+ 10
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 8x6+ 8x2+ 30 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 4x2+ 18
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 8x6+ 16x5+ 8x2+ 14 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 8x+ 14
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 16x6+ 14 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 30
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 4x4+ 26 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 8x2+ 8x+ 22
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 16x6+ 8x2+ 6 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 12x2+ 10
|
| 30 | 8 | 1 | -1 | i | x8+ 16x7+ 16x5+ 56 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 30
|
| 30 | 8 | 1 | -1 | i | x8+ 12x6+ 10x4+ 4x2+ 15 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 4x2+ 10
|
| 30 | 8 | 1 | -1 | -i | x8+ 28x6+ 6x4+ 4x2+ 31 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 8x+ 6
|
| 30 | 8 | 1 | -1 | i | x8+ 12x6+ 30x4+ 4x2+ 7 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 8x2+ 8x+ 22
|
| 30 | 8 | 1 | -1 | -i | x8+ 28x6+ 6x4+ 28x2+ 31 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 30
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 8x2+ 22 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 8x2+ 8x+ 22
|
| 30 | 8 | 1 | -1 | i | x8+ 28x6+ 6x4+ 20x2+ 23 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 8x+ 14
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 16x6+ 4x4+ 10 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 12x2+ 10
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x6+ 4x4+ 60 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 14
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 12x4+ 2 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 8x+ 14
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 8x4+ 14 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 30
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 12x4+ 26 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 8x+ 6
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 14
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 20x4+ 8x2+ 16x+ 2 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 14
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 16x5+ 24x4+ 16x2+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 14
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 16x+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 14
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 8x6+ 8x2+ 22 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 4x2+ 10
|
| 30 | 8 | 1 | -1 | i | x8+ 12x6+ 6x4+ 20x2+ 31 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 8x+ 6
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 16x3+ 8x2+ 6 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 12x2+ 10
|
| 30 | 8 | 1 | -1 | i | x8+ 12x6+ 26x4+ 4x2+ 7 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 4x2+ 18
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 24x2+ 16x+ 14 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 12x2+ 18
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 16x5+ 4x4+ 16x3+ 24x2+ 18 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 30
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 16x4+ 14 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 30
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 14 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 30
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 12x4+ 10 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 4x2+ 10
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 8x2+ 30 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 12x2+ 2
|
| 30 | 8 | 1 | -1 | -i | x8+ 20x6+ 14x4+ 4x2+ 23 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 14
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 24x4+ 14 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 30
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 28x4+ 10 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 4x2+ 10
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 24x6+ 16x5+ 8x2+ 14 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 8x+ 14
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 16x5+ 24x2+ 16x+ 30 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 12x2+ 2
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 4x4+ 18 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 12x2+ 18
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 16x4+ 8x2+ 14 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 12x2+ 18
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 16x4+ 8x2+ 22 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 8x2+ 8x+ 22
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 16x6+ 28x4+ 26 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 8x+ 6
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 8x2+ 14 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 12x2+ 18
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 24x6+ 28x4+ 2 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 12x2+ 2
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 20x4+ 2 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 12x2+ 2
|
| 30 | 8 | 1 | -1 | -i | x8+ 28x6+ 26x4+ 20x2+ 7 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 4x2+ 18
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 16x6+ 16x4+ 30 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2 | x4+ 14
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 16x+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 22
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 8x6+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 22
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 22
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 16x6+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6
|
| 30 | 8 | 1 | -1 | i | x8+ 12x6+ 6x4+ 12x2+ 7 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 16x+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6
|
| 30 | 8 | 1 | -1 | i | x8+ 4x6+ 14x4+ 20x2+ 31 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 22
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 24x6+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 22
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 16x2+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6
|
| 30 | 8 | 1 | -1 | -i | x8+ 8x7+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6
|
| 30 | 8 | 1 | -1 | i | x8+ 16x6+ 16x5+ 88 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 22
|
| 30 | 8 | 1 | -1 | -i | x8+ 16x5+ 32x4+ 24 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 8x4+ 22 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6
|
| 30 | 8 | 1 | -1 | -i | x8+ 28x6+ 22x4+ 28x2+ 23 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 6
|
| 30 | 8 | 1 | -1 | i | x8+ 8x7+ 8x4+ 6 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 22
|
| 30 | 8 | 1 | -1 | -i | x8+ 20x6+ 14x4+ 4x2+ 31 | T30
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | | | |
| 137/32 | 2* | x4+ 22
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 24x6+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 10
|
| 30 | 8 | 1 | -* | -i | x8+ 8x6+ 60x4+ 108 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 26
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 16x3+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 18
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x5+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 18
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 8x6+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 8x6+ 16x5+ 16x3+ 24x2+ 16x+ 2 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 12x2+ 6
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 8x6+ 16x5+ 16x+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 16x6+ 16x5+ 16x+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 18
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x5+ 16x4+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 18
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x6+ 26 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 26
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 10
|
| 30 | 8 | 1 | -* | i | x8+ 12x6+ 6x4+ 20x2+ 3 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 8x+ 10
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 24x6+ 4x4+ 6 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 4x2+ 6
|
| 30 | 8 | 1 | -* | -i | x8+ 28x6+ 6x4+ 4x2+ 3 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 8x+ 10
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 8x2+ 18 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 4x2+ 6
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 8x6+ 16x5+ 12x4+ 16x2+ 16x+ 14 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 8x+ 10
|
| 30 | 8 | 1 | -* | -i | x8+ 28x6+ 22x4+ 4x2+ 19 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 8x+ 10
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 8x6+ 16x3+ 26 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 26
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x5+ 16x2+ 16x+ 26 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 26
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 8x2+ 26 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 4x2+ 14
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 28x4+ 6 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 4x2+ 6
|
| 30 | 8 | 1 | -* | -i | x8+ 16x5+ 24x4+ 88 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 12x2+ 6
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 24x6+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 16x4+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 10
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 16x3+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 4x4+ 30 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 8x+ 10
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 12x4+ 14 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 4x2+ 14
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 18
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 8x6+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 10
|
| 30 | 8 | 1 | -* | i | x8+ 8x6+ 4x4+ 12 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 4x2+ 14
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 4x4+ 6 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 12x2+ 6
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 20x4+ 22 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 12x2+ 6
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 24x6+ 16x2+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 10
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x3+ 16x2+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 20x4+ 30 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 8x+ 10
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x6+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 10
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 8x4+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 18
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x6+ 12x4+ 8x2+ 6 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 18
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 4x4+ 16x+ 6 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 12x2+ 6
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 16x5+ 12x4+ 16x3+ 14 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 4x2+ 14
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 8x6+ 4x4+ 16x+ 22 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 4x2+ 6
|
| 30 | 8 | 1 | -* | i | x8+ 12x6+ 26x4+ 4x2+ 3 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 4x2+ 14
|
| 30 | 8 | 1 | -* | -i | x8+ 20x6+ 18x4+ 12x2+ 3 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 12x2+ 6
|
| 30 | 8 | 1 | -* | i | x8+ 4x6+ 18x4+ 28x2+ 3 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 12x2+ 6
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x3+ 8x2+ 18 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 4x2+ 6
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x6+ 4x4+ 16x3+ 16x2+ 30 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 8x+ 10
|
| 30 | 8 | 1 | -* | -i | x8+ 12x6+ 22x4+ 12x2+ 19 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2
|
| 30 | 8 | 1 | -* | -i | x8+ 4x6+ 26x4+ 12x2+ 11 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 4x2+ 6
|
| 30 | 8 | 1 | -* | -i | x8+ 4x6+ 10x4+ 12x2+ 3 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 4x2+ 14
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x6+ 16x2+ 16x+ 2 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 2
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x2+ 10 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 10
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 8x2+ 2 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 4x2+ 6
|
| 30 | 8 | 1 | -* | i | x8+ 12x6+ 22x4+ 20x2+ 19 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 8x+ 10
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 24x6+ 24x2+ 16x+ 2 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 12x2+ 6
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 8x6+ 26 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 26
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 12x4+ 22 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 4x2+ 6
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 12x4+ 30 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 4x2+ 14
|
| 30 | 8 | 1 | -* | i | x8+ 56x6+ 60x4+ 44 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 10
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 16x+ 18 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2 | x4+ 18
|
| 30 | 8 | 1 | -* | i | x8+ 8x7+ 16x5+ 26 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 26
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 8x2+ 10 | T35
| $((C_8\times C_2):C_2):C_2$
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 4x2+ 14
|
| 30 | 8 | 1 | -* | -i | x8+ 20x6+ 14x4+ 4x2+ 19 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 26
|
| 30 | 8 | 1 | -* | -i | x8+ 8x7+ 26 | T35
| T30
|
| [2, 3, 7/2, 4, 17/4, 19/4] | 2 | | |
| 137/32 | -2* | x4+ 26
|
|
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 4x4+ 16x2+ 50 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x6+ 4x4+ 16x2+ 34 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 4x4+ 16x2+ 18 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x4+ 8x2+ 16x+ 46 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 4x4+ 16x2+ 34 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 16x7+ 28x4+ 16x3+ 2 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 28x4+ 16x3+ 50 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x6+ 4x4+ 16x2+ 2 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 12x4+ 18 | $C_8:C_2$
| $C_{8}$
|
| 31/8 | 2 | x4+ 4x2+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x6+ 12x4+ 2 | $C_8:C_2$
| $C_{8}$
|
| 31/8 | 2 | x4+ 8x+ 14
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 28x4+ 18 | $C_8:C_2$
| $C_{8}$
|
| 31/8 | 2 | x4+ 4x2+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 12x4+ 2 | $C_8:C_2$
| $C_{8}$
|
| 31/8 | 2 | x4+ 8x+ 14
|
| 31 | 8 | 1 | 2 | 1 | x8+ 18 | $D_8$
| $D_8$
|
| 4 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 2 | $D_8$
| $D_8$
|
| 4 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 34 | $D_8$
| $D_8$
|
| 4 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 50 | $D_8$
| $D_8$
|
| 4 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | -1 | x8+ 16x5+ 12x4+ 16x3+ 2 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | 2 | -1 | x8+ 20x4+ 16x3+ 50 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2 | x4+ 4x2+ 18
|
| 31 | 8 | 1 | 2 | -1 | x8+ 24x6+ 16x5+ 28x4+ 50 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2 | x4+ 4x2+ 18
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x6+ 4x4+ 50 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | 2 | -1 | x8+ 16x5+ 24x2+ 16x+ 14 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2 | x4+ 8x+ 14
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x6+ 4x4+ 2 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | 2 | -1 | x8+ 4x4+ 16x3+ 34 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2 | x4+ 8x+ 14
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x6+ 4x4+ 18 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x4+ 2 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 4 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 16x2+ 50 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 4 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x4+ 18 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 4 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 16x2+ 2 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 4 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 4x4+ 50 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2 | x4+ 4x2+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 4x4+ 18 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2 | x4+ 4x2+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 4x4+ 34 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2 | x4+ 8x+ 14
|
| 31 | 8 | 1 | 2 | 1 | x8+ 4x4+ 2 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2 | x4+ 8x+ 14
|
| 31 | 8 | 1 | 2 | -1 | x8+ 12x4+ 34 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | 2 | -1 | x8+ 12x4+ 18 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | 2 | -1 | x8+ 12x4+ 50 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | 2 | -1 | x8+ 12x4+ 2 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | 2 | -1 | x8+ 16x5+ 16x3+ 50 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 34 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x6+ 8x4+ 16x2+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | -1 | x8+ 16x7+ 8x4+ 16x3+ 16x2+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | -1 | x8+ 24x6+ 16x5+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 50 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | -1 | x8+ 24x6+ 16x2+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x6+ 8x4+ 16x2+ 50 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 16x3+ 34 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x6+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 2 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | -1 | x8+ 4x4+ 16x3+ 8x2+ 16x+ 6 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x6+ 34 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 2
|
| 31 | 8 | 1 | 2 | -1 | x8+ 16x7+ 8x6+ 16x2+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | 1 | x8+ 16x3+ 18 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2 | x4+ 18
|
| 31 | 8 | 1 | 2 | -1 | x8+ 28x4+ 24x2+ 50 | T28
| T28
|
| 141/32 | 2 | x4+ 14
|
| 31 | 8 | 1 | 2 | -1 | x8+ 28x4+ 24x2+ 18 | T28
| T28
|
| 141/32 | 2 | x4+ 14
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 20x4+ 8x2+ 50 | T28
| T28
|
| 141/32 | 2 | x4+ 30
|
| 31 | 8 | 1 | 2 | 1 | x8+ 4x4+ 8x2+ 2 | T28
| T28
|
| 141/32 | 2 | x4+ 14
|
| 31 | 8 | 1 | 2 | 1 | x8+ 4x4+ 8x2+ 18 | T28
| T28
|
| 141/32 | 2 | x4+ 30
|
| 31 | 8 | 1 | 2 | -1 | x8+ 12x4+ 24x2+ 2 | T28
| T28
|
| 141/32 | 2 | x4+ 30
|
| 31 | 8 | 1 | 2 | -1 | x8+ 24x6+ 20x4+ 8x2+ 2 | T28
| T28
|
| 141/32 | 2 | x4+ 14
|
| 31 | 8 | 1 | 2 | 1 | x8+ 16x3+ 16x+ 14 | T28
| T28
|
| 141/32 | 2 | x4+ 14
|
| 31 | 8 | 1 | 2 | 1 | x8+ 16x+ 14 | T28
| T28
|
| 141/32 | 2 | x4+ 14
|
| 31 | 8 | 1 | 2 | 1 | x8+ 12x4+ 8x2+ 18 | T28
| T28
|
| 141/32 | 2 | x4+ 14
|
| 31 | 8 | 1 | 2 | 1 | x8+ 16x+ 62 | T28
| T28
|
| 141/32 | 2 | x4+ 30
|
| 31 | 8 | 1 | 2 | -1 | x8+ 24x6+ 20x4+ 8x2+ 50 | T28
| T28
|
| 141/32 | 2 | x4+ 30
|
| 31 | 8 | 1 | 2 | -1 | x8+ 4x4+ 24x2+ 2 | T28
| T28
|
| 141/32 | 2 | x4+ 14
|
| 31 | 8 | 1 | 2 | -1 | x8+ 16x6+ 16x+ 62 | T28
| T28
|
| 141/32 | 2 | x4+ 30
|
| 31 | 8 | 1 | 2 | 1 | x8+ 32x5+ 480 | T28
| T28
|
| 141/32 | 2 | x4+ 30
|
| 31 | 8 | 1 | 2 | -1 | x8+ 24x6+ 20x4+ 8x2+ 18 | T28
| T28
|
| 141/32 | 2 | x4+ 30
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x6+ 16x5+ 16x3+ 8x2+ 2 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x2+ 18 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x2+ 2 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | 2 | -1 | x8+ 16x6+ 8x4+ 8x2+ 34 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x2+ 34 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x6+ 24x2+ 34 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x2+ 50 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x4+ 8x2+ 18 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | 2 | 1 | x8+ 8x4+ 8x2+ 2 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x6+ 8x2+ 18 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x6+ 8x2+ 2 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | 2 | 1 | x8+ 24x2+ 18 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x2+ 2 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | 2 | -1 | x8+ 24x6+ 72 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x2+ 34 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | 2 | -1 | x8+ 8x4+ 24x2+ 50 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x6+ 12x4+ 10 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x6+ 12x4+ 26 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x6+ 32x3+ 24 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x6+ 12x4+ 42 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x6+ 12x4+ 26 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x6+ 12x4+ 42 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x6+ 12x4+ 58 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x6+ 12x4+ 58 | $C_{8}$
| $C_{8}$
|
| 31/8 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x6+ 4x4+ 16x2+ 10 | $C_8:C_2$
| $C_{8}$
|
| 31/8 | 2* | x4+ 12x2+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x6+ 20x4+ 16x2+ 26 | $C_8:C_2$
| $C_{8}$
|
| 31/8 | 2* | x4+ 8x2+ 8x+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 12x4+ 16x3+ 10 | $C_8:C_2$
| $C_{8}$
|
| 31/8 | 2* | x4+ 12x2+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x6+ 20x4+ 16x2+ 26 | $C_8:C_2$
| $C_{8}$
|
| 31/8 | 2* | x4+ 8x2+ 8x+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x4+ 10 | $QD_{16}$
| $QD_{16}$
|
| 4 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x4+ 58 | $QD_{16}$
| $QD_{16}$
|
| 4 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x4+ 26 | $QD_{16}$
| $QD_{16}$
|
| 4 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x4+ 10 | $QD_{16}$
| $QD_{16}$
|
| 4 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | 1 | x8+ 16x5+ 24x2+ 16x+ 6 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x6+ 20x4+ 58 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2* | x4+ 8x2+ 8x+ 22
|
| 31 | 8 | 1 | 2* | 1 | x8+ 4x4+ 16x3+ 42 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 24x6+ 32x3+ 152 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x6+ 12x4+ 16x2+ 58 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | 2* | 1 | x8+ 24x6+ 20x4+ 42 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2* | x4+ 12x2+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x6+ 4x4+ 10 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2* | x4+ 12x2+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x6+ 20x4+ 26 | $C_8:C_2$
| $C_8:C_2$
|
| 4 | 2* | x4+ 8x2+ 8x+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 10 | $(C_8\times C_2):C_2$
| $D_8$
|
| 4 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 26 | $(C_8\times C_2):C_2$
| $D_8$
|
| 4 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | -1 | x8+ 42 | $(C_8\times C_2):C_2$
| $D_8$
|
| 4 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 58 | $(C_8\times C_2):C_2$
| $D_8$
|
| 4 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | -1 | x8+ 4x4+ 42 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 12x4+ 58 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2* | x4+ 8x2+ 8x+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 4x4+ 58 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | 2* | 1 | x8+ 12x4+ 10 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2* | x4+ 12x2+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 12x4+ 42 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2* | x4+ 12x2+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 4x4+ 10 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 4x4+ 26 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | 2* | 1 | x8+ 12x4+ 26 | $(C_8:C_2):C_2$
| $(C_8:C_2):C_2$
|
| 67/16 | 2* | x4+ 8x2+ 8x+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x6+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 24x6+ 16x5+ 58 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x6+ 8x4+ 16x2+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x6+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | -1 | x8+ 16x3+ 58 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | 1 | x8+ 16x5+ 16x3+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | 1 | x8+ 24x6+ 8x4+ 16x2+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x6+ 58 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | 1 | x8+ 24x6+ 8x4+ 16x2+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x6+ 8x4+ 16x2+ 58 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x6+ 10 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x6+ 42 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x6+ 42 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x6+ 16x2+ 42 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 16x7+ 96x2+ 232 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 16x3+ 26 | $C_4^2:C_2$
| $C_4^2:C_2$
|
| 67/16 | -2* | x4+ 26
|
| 31 | 8 | 1 | 2* | -1 | x8+ 32x3+ 216 | T28
| T28
|
| 141/32 | 2* | x4+ 6
|
| 31 | 8 | 1 | 2* | 1 | x8+ 12x4+ 24x2+ 26 | T28
| T28
|
| 141/32 | 2* | x4+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 16x+ 54 | T28
| T28
|
| 141/32 | 2* | x4+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 4x4+ 8x2+ 10 | T28
| T28
|
| 141/32 | 2* | x4+ 22
|
| 31 | 8 | 1 | 2* | 1 | x8+ 12x4+ 24x2+ 10 | T28
| T28
|
| 141/32 | 2* | x4+ 6
|
| 31 | 8 | 1 | 2* | 1 | x8+ 24x6+ 4x4+ 8x2+ 58 | T28
| T28
|
| 141/32 | 2* | x4+ 6
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x6+ 40x4+ 40 | T28
| T28
|
| 141/32 | 2* | x4+ 6
|
| 31 | 8 | 1 | 2* | 1 | x8+ 24x6+ 4x4+ 8x2+ 42 | T28
| T28
|
| 141/32 | 2* | x4+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 4x4+ 8x2+ 26 | T28
| T28
|
| 141/32 | 2* | x4+ 6
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x4+ 16x+ 22 | T28
| T28
|
| 141/32 | 2* | x4+ 22
|
| 31 | 8 | 1 | 2* | 1 | x8+ 24x6+ 4x4+ 8x2+ 26 | T28
| T28
|
| 141/32 | 2* | x4+ 6
|
| 31 | 8 | 1 | 2* | 1 | x8+ 16x2+ 16x+ 22 | T28
| T28
|
| 141/32 | 2* | x4+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 16x3+ 16x+ 54 | T28
| T28
|
| 141/32 | 2* | x4+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 16x+ 38 | T28
| T28
|
| 141/32 | 2* | x4+ 6
|
| 31 | 8 | 1 | 2* | 1 | x8+ 12x4+ 24x2+ 42 | T28
| T28
|
| 141/32 | 2* | x4+ 6
|
| 31 | 8 | 1 | 2* | -1 | x8+ 16x+ 22 | T28
| T28
|
| 141/32 | 2* | x4+ 22
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x2+ 42 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x2+ 58 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x2+ 26 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x4+ 8x2+ 26 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x6+ 16x4+ 168 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | 2* | -1 | x8+ 4x4+ 16x+ 62 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x6+ 8x2+ 58 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x6+ 8x2+ 10 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | 2* | 1 | x8+ 24x6+ 40 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x2+ 10 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x4+ 24x2+ 10 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x2+ 10 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | 2* | 1 | x8+ 24x6+ 104 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | 2* | -1 | x8+ 24x6+ 8x2+ 42 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | 2* | -1 | x8+ 8x4+ 8x2+ 10 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | 2* | 1 | x8+ 8x2+ 26 | T35
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | -2 | -i | x8+ 4x4+ 16x3+ 14 | $D_8$
| $C_{8}$
|
| 31/8 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x6+ 4x4+ 14 | $QD_{16}$
| $C_{8}$
|
| 31/8 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | -2 | -i | x8+ 24x6+ 12x4+ 16x2+ 14 | $D_8$
| $C_{8}$
|
| 31/8 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 16x5+ 24x2+ 16x+ 26 | $QD_{16}$
| $C_{8}$
|
| 31/8 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | -2 | -i | x8+ 46 | $QD_{16}$
| $QD_{16}$
|
| 4 | 2 | x4+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x4+ 30 | $D_8$
| $D_8$
|
| 4 | 2 | x4+ 30
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x4+ 46 | $D_8$
| $D_8$
|
| 4 | 2 | x4+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 62 | $QD_{16}$
| $QD_{16}$
|
| 4 | 2 | x4+ 30
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x4+ 62 | $D_8$
| $D_8$
|
| 4 | 2 | x4+ 30
|
| 31 | 8 | 1 | -2 | -i | x8+ 30 | $QD_{16}$
| $QD_{16}$
|
| 4 | 2 | x4+ 30
|
| 31 | 8 | 1 | -2 | -i | x8+ 14 | $QD_{16}$
| $QD_{16}$
|
| 4 | 2 | x4+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x4+ 14 | $D_8$
| $D_8$
|
| 4 | 2 | x4+ 14
|
| 31 | 8 | 1 | -2 | i | x8+ 24x6+ 28x4+ 14 | $(C_8\times C_2):C_2$
| $C_8:C_2$
|
| 4 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | -2 | i | x8+ 8x6+ 28x4+ 14 | $(C_8\times C_2):C_2$
| $C_8:C_2$
|
| 4 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | -2 | i | x8+ 16x6+ 24x2+ 16x+ 10 | $(C_8\times C_2):C_2$
| $C_8:C_2$
|
| 4 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | -2 | i | x8+ 24x6+ 20x4+ 16x2+ 14 | $(C_8\times C_2):C_2$
| $C_8:C_2$
|
| 4 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | -2 | -i | x8+ 12x4+ 30 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | -2 | -i | x8+ 24x6+ 30 | T26
| $C_4^2:C_2$
|
| 67/16 | 2 | x4+ 14
|
| 31 | 8 | 1 | -2 | i | x8+ 8x6+ 8x4+ 16x2+ 14 | T26
| $C_4^2:C_2$
|
| 67/16 | 2 | x4+ 30
|
| 31 | 8 | 1 | -2 | i | x8+ 16x7+ 16x6+ 16x3+ 16x2+ 14 | T26
| $C_4^2:C_2$
|
| 67/16 | 2 | x4+ 14
|
| 31 | 8 | 1 | -2 | i | x8+ 20x4+ 30 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x6+ 30 | T26
| $C_4^2:C_2$
|
| 67/16 | 2 | x4+ 14
|
| 31 | 8 | 1 | -2 | i | x8+ 4x4+ 30 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 16x3+ 30 | T26
| $C_4^2:C_2$
|
| 67/16 | 2 | x4+ 30
|
| 31 | 8 | 1 | -2 | i | x8+ 20x4+ 46 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 12x4+ 14 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | -2 | -i | x8+ 28x4+ 14 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | -2 | i | x8+ 20x4+ 14 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2* | x4+ 4x2+ 14
|
| 31 | 8 | 1 | -2 | i | x8+ 8x6+ 8x4+ 16x2+ 30 | T26
| $C_4^2:C_2$
|
| 67/16 | 2 | x4+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 28x4+ 30 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2* | x4+ 8x+ 10
|
| 31 | 8 | 1 | -2 | i | x8+ 24x6+ 8x4+ 16x2+ 14 | T26
| $C_4^2:C_2$
|
| 67/16 | 2 | x4+ 30
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x6+ 14 | T26
| $C_4^2:C_2$
|
| 67/16 | 2 | x4+ 30
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x2+ 30 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 4x2+ 18
|
| 31 | 8 | 1 | -2 | -i | x8+ 28x4+ 16x+ 2 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | -2 | i | x8+ 8x4+ 8x2+ 30 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | -2 | i | x8+ 24x2+ 46 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 8x+ 14
|
| 31 | 8 | 1 | -2 | i | x8+ 24x2+ 30 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 4x2+ 18
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x2+ 14 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 8x+ 14
|
| 31 | 8 | 1 | -2 | i | x8+ 8x4+ 8x2+ 62 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | -2 | i | x8+ 24x6+ 8x2+ 46 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x2+ 62 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 4x2+ 18
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x6+ 8x2+ 14 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | -2 | i | x8+ 24x2+ 14 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 8x+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x6+ 8x2+ 46 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x6+ 8x2+ 62 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 12x2+ 2
|
| 31 | 8 | 1 | -2 | i | x8+ 8x4+ 8x2+ 14 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 12x2+ 18
|
| 31 | 8 | 1 | -2 | i | x8+ 24x2+ 62 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 4x2+ 18
|
| 31 | 8 | 1 | -2 | -i | x8+ 8x2+ 46 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2 | x4+ 8x+ 14
|
| 31 | 8 | 1 | -2 | -i | x8+ 20x4+ 16x3+ 24x2+ 30 | T35
| T28
|
| 141/32 | -2* | x4+ 26
|
| 31 | 8 | 1 | -2 | -i | x8+ 16x+ 10 | T35
| T28
|
| 141/32 | -2* | x4+ 10
|
| 31 | 8 | 1 | -2 | i | x8+ 16x6+ 16x+ 10 | T35
| T28
|
| 141/32 | -2* | x4+ 10
|
| 31 | 8 | 1 | -2 | -i | x8+ 16x+ 58 | T35
| T28
|
| 141/32 | -2* | x4+ 26
|
| 31 | 8 | 1 | -2 | -i | x8+ 16x+ 26 | T35
| T28
|
| 141/32 | -2* | x4+ 26
|
| 31 | 8 | 1 | -2 | i | x8+ 24x6+ 16x+ 26 | T35
| T28
|
| 141/32 | -2* | x4+ 26
|
| 31 | 8 | 1 | -2 | i | x8+ 16x6+ 16x+ 58 | T35
| T28
|
| 141/32 | -2* | x4+ 26
|
| 31 | 8 | 1 | -2 | -i | x8+ 28x4+ 24x2+ 62 | T35
| T28
|
| 141/32 | -2* | x4+ 26
|
| 31 | 8 | 1 | -2 | i | x8+ 20x4+ 8x2+ 46 | T35
| T28
|
| 141/32 | -2* | x4+ 10
|
| 31 | 8 | 1 | -2 | i | x8+ 8x4+ 16x+ 26 | T35
| T28
|
| 141/32 | -2* | x4+ 10
|
| 31 | 8 | 1 | -2 | -i | x8+ 24x6+ 40x4+ 56 | T35
| T28
|
| 141/32 | -2* | x4+ 10
|
| 31 | 8 | 1 | -2 | i | x8+ 28x4+ 8x2+ 62 | T35
| T28
|
| 141/32 | -2* | x4+ 26
|
| 31 | 8 | 1 | -2 | -i | x8+ 16x+ 42 | T35
| T28
|
| 141/32 | -2* | x4+ 10
|
| 31 | 8 | 1 | -2 | i | x8+ 12x4+ 8x2+ 14 | T35
| T28
|
| 141/32 | -2* | x4+ 10
|
| 31 | 8 | 1 | -2 | -i | x8+ 24x6+ 12x4+ 8x2+ 30 | T35
| T28
|
| 141/32 | -2* | x4+ 10
|
| 31 | 8 | 1 | -2 | i | x8+ 16x6+ 28x4+ 24x2+ 30 | T35
| T28
|
| 141/32 | -2* | x4+ 26
|
| 31 | 8 | 1 | -2* | i | x8+ 16x4+ 8x2+ 16x+ 18 | $D_8$
| $C_{8}$
|
| 31/8 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 8x6+ 16x3+ 8x2+ 16x+ 2 | $QD_{16}$
| $C_{8}$
|
| 31/8 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 8x2+ 16x+ 18 | $D_8$
| $C_{8}$
|
| 31/8 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 4x4+ 16x3+ 6 | $QD_{16}$
| $C_{8}$
|
| 31/8 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 96 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 4 | 2* | x4+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 8x4+ 38 | $(C_8\times C_2):C_2$
| $D_8$
|
| 4 | 2* | x4+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 16x7+ 16x6+ 24x2+ 16x+ 2 | $(C_8\times C_2):C_2$
| $C_8:C_2$
|
| 4 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x6+ 4x4+ 16x2+ 6 | $(C_8\times C_2):C_2$
| $C_8:C_2$
|
| 4 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 24 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 4 | 2* | x4+ 22
|
| 31 | 8 | 1 | -2* | i | x8+ 8x4+ 54 | $(C_8\times C_2):C_2$
| $D_8$
|
| 4 | 2* | x4+ 22
|
| 31 | 8 | 1 | -2* | i | x8+ 16x5+ 6 | $(C_8\times C_2):C_2$
| $D_8$
|
| 4 | 2* | x4+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x6+ 12x4+ 6 | $(C_8\times C_2):C_2$
| $C_8:C_2$
|
| 4 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 24x6+ 12x4+ 6 | $(C_8\times C_2):C_2$
| $C_8:C_2$
|
| 4 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 6 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 4 | 2* | x4+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 384 | $(C_8\times C_2):C_2$
| $QD_{16}$
|
| 4 | 2* | x4+ 22
|
| 31 | 8 | 1 | -2* | i | x8+ 16x5+ 22 | $(C_8\times C_2):C_2$
| $D_8$
|
| 4 | 2* | x4+ 22
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x6+ 16x2+ 6 | T26
| $C_4^2:C_2$
|
| 67/16 | 2* | x4+ 22
|
| 31 | 8 | 1 | -2* | i | x8+ 12x4+ 22 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 8x6+ 22 | T26
| $C_4^2:C_2$
|
| 67/16 | 2* | x4+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x6+ 16x5+ 6 | T26
| $C_4^2:C_2$
|
| 67/16 | 2* | x4+ 22
|
| 31 | 8 | 1 | -2* | -i | x8+ 24x6+ 8x4+ 16x2+ 22 | T26
| $C_4^2:C_2$
|
| 67/16 | 2* | x4+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 20x4+ 6 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 4x4+ 54 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 28x4+ 22 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 4x4+ 6 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 16x3+ 6 | T26
| $C_4^2:C_2$
|
| 67/16 | 2* | x4+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 24x6+ 16x2+ 22 | T26
| $C_4^2:C_2$
|
| 67/16 | 2* | x4+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 12x4+ 6 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 16x3+ 22 | T26
| $C_4^2:C_2$
|
| 67/16 | 2* | x4+ 22
|
| 31 | 8 | 1 | -2* | i | x8+ 8x6+ 6 | T26
| $C_4^2:C_2$
|
| 67/16 | 2* | x4+ 22
|
| 31 | 8 | 1 | -2* | -i | x8+ 20x4+ 54 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2 | x4+ 4x2+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 28x4+ 6 | T26
| $(C_8:C_2):C_2$
|
| 67/16 | -2 | x4+ 12x2+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x4+ 8x2+ 38 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 12x2+ 10
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x4+ 8x2+ 22 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 8x2+ 8x+ 22
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x4+ 8x2+ 54 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 8x2+ 8x+ 22
|
| 31 | 8 | 1 | -2* | i | x8+ 8x2+ 6 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 8x2+ 54 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | -2* | i | x8+ 16x6+ 8x4+ 8x2+ 54 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 8x2+ 8x+ 22
|
| 31 | 8 | 1 | -2* | -i | x8+ 24x2+ 54 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x6+ 88 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | -2* | i | x8+ 8x6+ 8x2+ 38 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 12x2+ 10
|
| 31 | 8 | 1 | -2* | -i | x8+ 24x2+ 22 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | -2* | i | x8+ 8x2+ 22 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 4x2+ 10
|
| 31 | 8 | 1 | -2* | i | x8+ 24x6+ 16x5+ 8x2+ 54 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 8x2+ 8x+ 22
|
| 31 | 8 | 1 | -2* | i | x8+ 8x2+ 38 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x4+ 8x2+ 6 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 12x2+ 10
|
| 31 | 8 | 1 | -2* | i | x8+ 16x5+ 8x4+ 24x2+ 6 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 12x2+ 10
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x6+ 216 | $((C_8\times C_2):C_2):C_2$
| $((C_8\times C_2):C_2):C_2$
|
| 141/32 | 2* | x4+ 8x+ 6
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x6+ 8x4+ 16x+ 2 | T35
| T28
|
| 141/32 | -2 | x4+ 18
|
| 31 | 8 | 1 | -2* | -i | x8+ 16x7+ 16x5+ 16x+ 2 | T35
| T28
|
| 141/32 | -2 | x4+ 2
|
| 31 | 8 | 1 | -2* | -i | x8+ 16x2+ 16x+ 50 | T35
| T28
|
| 141/32 | -2 | x4+ 18
|
| 31 | 8 | 1 | -2* | i | x8+ 12x4+ 24x2+ 6 | T35
| T28
|
| 141/32 | -2 | x4+ 2
|
| 31 | 8 | 1 | -2* | -i | x8+ 28x4+ 8x2+ 38 | T35
| T28
|
| 141/32 | -2 | x4+ 2
|
| 31 | 8 | 1 | -2* | i | x8+ 16x+ 50 | T35
| T28
|
| 141/32 | -2 | x4+ 18
|
| 31 | 8 | 1 | -2* | -i | x8+ 16x6+ 16x5+ 16x+ 2 | T35
| T28
|
| 141/32 | -2 | x4+ 2
|
| 31 | 8 | 1 | -2* | -i | x8+ 16x6+ 16x+ 50 | T35
| T28
|
| 141/32 | -2 | x4+ 18
|
| 31 | 8 | 1 | -2* | i | x8+ 16x+ 34 | T35
| T28
|
| 141/32 | -2 | x4+ 2
|
| 31 | 8 | 1 | -2* | i | x8+ 24x6+ 28x4+ 8x2+ 6 | T35
| T28
|
| 141/32 | -2 | x4+ 18
|
| 31 | 8 | 1 | -2* | i | x8+ 16x+ 18 | T35
| T28
|
| 141/32 | -2 | x4+ 18
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x4+ 16x+ 2 | T35
| T28
|
| 141/32 | -2 | x4+ 18
|
| 31 | 8 | 1 | -2* | i | x8+ 16x+ 2 | T35
| T28
|
| 141/32 | -2 | x4+ 2
|
| 31 | 8 | 1 | -2* | i | x8+ 24x6+ 28x4+ 8x2+ 38 | T35
| T28
|
| 141/32 | -2 | x4+ 18
|
| 31 | 8 | 1 | -2* | -i | x8+ 8x6+ 28x4+ 8x2+ 22 | T35
| T28
|
| 141/32 | -2 | x4+ 2
|
| 31 | 8 | 1 | -2* | i | x8+ 16x3+ 16x+ 2 | T35
| T28
|
| 141/32 | -2 | x4+ 2
|